Ask Ethan: Why Is The Black Hole Information Loss Paradox A Problem?

It was Stephen Hawking’s obsession for the last 30 years of his life. Here’s why it matters.
When it comes to the sciences, sometimes making two observations or measurements that appear to contradict each other is the best thing that could possibly happen. These apparent paradoxes help lead the field forward, and show us where to look for the solution. The fact that the night sky is dark, Olbers’ paradox, wasn’t resolved until the Big Bang came along. The Fermi paradox helps us understand how rare intelligent, spacefaring civilizations must truly be. And the black hole information loss paradox might truly be the key to unlocking quantum gravity. But is that last one really true? Gabe Eisenstein is skeptical, asking:
Why do physicists all seem to agree that the information loss paradox is a real problem? It seems to depend on determinism, which seems incompatible with QM.
Many people have a lot of preconceptions when it comes to the black hole information paradox, so let’s give you the full version on why it’s such a problem, and what its solution would mean.

The first thing to recognize is that the black hole information paradox isn’t so much about information the way we conceive of it. When we think about words in a printed book, the number of bits and bytes in a computer file, or the configurations and quantum properties of the particles comprising a system, we think of information as the full suite of things we’d need to know in order to reconstruct, from scratch, whatever it is we began with.
But this conventional definition of information isn’t really a physical property that’s easily measurable or quantifiable the way that, say, temperature is. Luckily for us, there is a physical property that can be defined as equivalent to information: entropy. Instead of thinking of entropy as a measure of disorder, we should think about entropy as the amount of “missing” information needed to determine what the specific microstate of your system is.

There are rules that entropy must follow in this Universe. The second law of thermodynamics is one of the most inviolable ones: take any system you like, don’t allow anything to enter or leave it, and its entropy will never spontaneously decrease.
Eggs don’t spontaneously unscramble themselves, warm water never separates into hot and cold sections, and ashes don’t reassemble into the shape of the object they were before they were burned. All of these would be an example of decreasing entropy, and this doesn’t happen, in nature, on its own. Entropy can remain the same; under most circumstance it increases; but it can never return to a lower-entropy state.
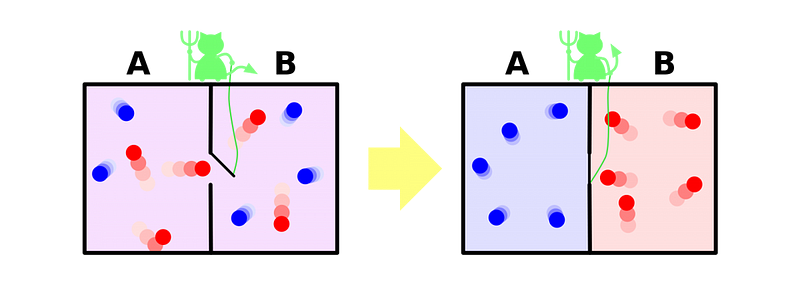
The only way to artificially decrease entropy is to pump energy into a system, “cheating” the second law by increasing the entropy external to the system by a larger amount than it decreases within your system. (Cleaning your house is one such example.) Put simply, entropy can never be destroyed.
So what happens, then, when a black hole feeds on matter? Let’s go back to our original thought, and imagine throwing a book into a black hole. The only properties we know to assign to a black hole are very straightforward: mass, charge, and angular momentum. The book contains information, but when you throw it into a black hole, it only increases the black hole’s mass. Originally, when it came to black holes, it was thought that their entropy must be zero. But if that were the case, allowing anything to fall into a black hole would always violate the second law of thermodynamics. And this, of course, cannot be.

So how, then, do you quantify the entropy of a black hole?
The idea for this can be traced back to John Wheeler, who was thinking about what happens to an object as it fall into a black hole from the point of view of an observer well outside the event horizon. From far away, someone falling in would appear to asymptotically approach the event horizon, turning redder and redder due to gravitational redshift, and taking an infinitely long time to reach the horizon, as relativistic time dilation took effect. The information, therefore, from whatever fell in would appear to be encoded on the surface area of the black hole itself.

This elegantly seems to solve the problem and make sense all at once. When something falls into a black hole, its mass increases. When its mass increases, so does its radius, and therefore, its surface area. The greater your surface area, the more information you can encode, the same way you can fit more strokes of a pen on a larger globe than a smaller one.
This implies that instead of an entropy of zero, a black hole’s entropy is enormous! Even though an event horizon is relatively small compared to the size of the Universe, the amount of space it takes to encode a quantum bit is tiny, and therefore a tremendous amount of information can be encoded onto a black hole’s surface. Entropy rises, information is conserved, and the laws of thermodynamics are obeyed. We can all go home.
Except, of course, for the paradox part.

You see, if black holes have an entropy, then they must also have a temperature. And like anything that has a temperature, it must radiate.
As Stephen Hawking famously demonstrated, black holes emit radiation of a particular (blackbody) spectrum and temperature, defined by the mass of the black hole that it’s coming from. Over time, that emission of energy means that the black hole is losing mass, owing to Einstein’s famous E = mc2; if energy is being released, it has to come from somewhere, and that “somewhere” must be the black hole itself. Over time, the black hole will lose mass faster and faster, until in a brilliant flash of light far in the future, it evaporates entirely.

But if the black hole evaporates into pure blackbody radiation, defined only by the black hole’s mass, then what happens to all that information and all that entropy that was encoded on the event horizon of the black hole? You can’t just destroy that information, can you?
That’s the root of the black hole information paradox. Black holes must have a large entropy, that entropy includes all the information about what created the black hole, the information gets encoded on the surface of the event horizon, but as the black hole decays away via Hawking radiation, the event horizon disappears, leaving only radiation in its place. That radiation, as far as we understand it, is only dependent on a black hole’s mass, not on anything else.

A book of gibberish and a copy of the Count of Monte Cristo contain different amounts of information. Yet, if their masses were identical, and we threw them into identical black holes, we’d eventually expect equivalent Hawking radiation to emerge from them. To an outside observer, it looks like information gets destroyed, and based on what we know about entropy, that shouldn’t be possible. That would, in fact, violate the 2nd law of thermodynamics.
If you burned those two identically-sized books instead, the patterns of ink on the paper, the variations in molecular structures, and other minute differences all contain information that could allow you to reconstruct the information within them. The information may be scrambled, but it’s not lost. The black hole information paradox, however, is a real problem. Once a black hole evaporates, that initial information has left no trace anywhere in our observable Universe.

We may not have the answers to this paradox yet, but it represents a real problem for physics. Still, we can envision what the solution to this might look like. As far as we understand it, one of two things must be happening:
- Either information is truly destroyed somehow when a black hole evaporates, teaching us that there are new physical rules and laws in place for black hole evaporation,
- Or the radiation that’s emitted somehow contains this information, meaning that there’s more to Hawking radiation than the calculations we’ve done so far imply.

Most people working on this problem think that somehow, there must be a way that the information encoded on the surface of the black hole imprints itself on the outgoing radiation. How that happens, though, is something no one understands. Is it does to the fact that information on the black hole’s surface applies quantum corrections to the purely thermal Hawking radiation state? It’s tempting to think so, but it’s unproven. As it stands, there are a myriad of hypothesized solutions to the paradox, but none have been proven.

The black hole information paradox is agnostic about whether the nature of the quantum Universe is deterministic or non-deterministic, which quantum interpretation you choose, whether there are hidden variables or not, or many other aspects of the nature of reality. We do not yet know whether there are more dimensions than the four we presently know of, and while many proposed solutions invoke the holographic principle, it is uncertain whether that plays any role in whatever the resolution of the paradox truly turns out to be.
Many ideas are compelling or interesting, but these are merely ideas; the paradox remains unresolved. There is no clear solution. Despite the fact that pretty much everyone agrees that the solution ought to have information encoded in the outgoing radiation, no one yet knows how to arrive at it. Until we can figure out how — or if — information is preserved in black hole decays, this puzzle will remain a great paradox of our time.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.




