Ask Ethan: Why Can’t Time Be Reversed For Three-Body Systems?

In principle, the laws of physics are the same forwards and backwards. But in practice, time only runs in one direction.

Most of the laws of physics are the same whether you run the clock forwards or backwards. A planet that revolves around a star appears to obey the same rules as it would if you recorded it and played the recording backwards. This is true for any gravitational, electromagnetic, or strong nuclear interaction between two particles: they are time-reversal invariant. Normally, we only see the non-reversible effects of chaos and thermodynamics with extremely large systems, but a recent paper claims to have shown this for the gravitational interaction with only three masses. Jonathan Belew wants to know what this means, asking:

Does this have any relevancy to the n-body problem, time-reversal symmetry as a whole, or implications for cosmology? Or is it theoretical and only apply to a small subset of cases that do not make up a significant portion of the observed universe?

Let’s unpack what it all means.

When you observe the Earth rotating on its axis and revolving around the Sun, you cannot tell, based on the observed dynamics alone, whether the clock is running forwards or backwards. This is because, for a system such as this, the relevant laws of physics appear to be perfectly time-reversal invariant. (NASA / MESSENGER MISSION)

It’s well-known that nearly all interactions in physics obey what we call time-reversal invariance. This means that the laws of physics behave the same way forwards or backwards. You can view this in a number of ways, such as:

running your clock forwards or backwards in time,
running all of your system’s particles from the beginning with their initial momenta or from the end with the opposite of their final momenta,
or starting from your final state and asking if there’s always a way to evolve that final state back into your initial state.

For any one or two particles experiencing any physical force or interaction, with the exception of the weak nuclear interaction (which is known to violate time-reversal symmetry), there’s always a way to recover your initial state if you begin with your final state and evolve it according to the known laws of physics.

By examining this strobe image of a bouncing ball, you cannot tell for certain whether the ball is moving towards the right and losing energy with each bounce, or whether it’s moving towards the left and getting an energetic kick with each bounce. The laws of physics are symmetric under time-reversal transformations, and the equations of motion will give you two solutions (positive and negative) to any trajectory you can derive. Only by imposing physical constraints can we know which of the two yields the correct answer. (WIKIMEDIA COMMONS USERS MICHAELMAGGS AND (EDITED BY) RICHARD BARTZ)

However, the macroscopic world doesn’t appear to be time-reversal invariant at all. Sure, if you watch a ball flying through the air, up or down a hill, Earth spinning on its axis, or a moon orbiting a planet, you can’t tell just from looking at it whether the clock is running forwards or backwards. Because the laws of physics are the same forwards and backwards in time — because of this time-reversal invariance — the same rules are obeyed.

But other phenomena clearly have a direction: an arrow of time. Drop a glass of water onto a hard floor and watch it shatter; the time-reversed reaction will never, ever occur, not even if you perform the experiment quadrillions of times. Scramble and cook and egg; an egg will never “uncook” and “unscramble” itself. These are examples where there’s clearly a preferred direction to the Universe, something we refer to as the thermodynamic arrow of time.

The history of the Universe and the arrow of time, which always flows forward in the same direction and at the same rate for any observer anywhere. Entropy always increases as well, and that’s called the thermodynamic arrow of time, but our perceptive arrow of time is not necessarily related. (NASA / GSFC)

Even though, in both of these cases, only gravitational and electromagnetic interactions are at play, the interactions become so complex and occur between so many particles — chaotically, on top of classically — that the final state you wind up with is extraordinarily unlikely to ever return to the initial state, no matter how intricately you reverse the reaction.

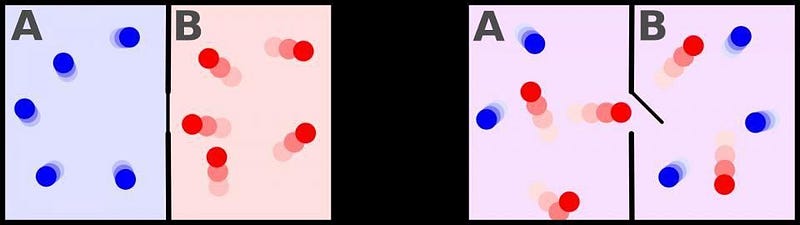
It’s like taking a room with a divider down the middle, where one side is hot and the other is cold, removing the divider, and watching the gas molecules fly around. In the absence of any other inputs, the two halves of the room will mix and equilibrate, reaching the same temperature. No matter what you did to those particles, including reverse all of their momenta, they’d never reach the half-hot and half-cold state ever again.

A system set up in the initial conditions on the left and let to evolve will become the system on the right spontaneously, gaining entropy in the process. A system starting in the left-most configuration will never spontaneously evolve to look like the system on the right. (WIKIMEDIA COMMONS USERS HTKYM AND DHOLLM)

This type of irreversibility is well understood for large, many particle systems, and is an essential part of the sciences of thermodynamics and statistical mechanics. It’s part of why we use the quantity of entropy so frequently, and our understanding of these processes helps us understand the second law of thermodynamics: that in a closed system, entropy only increases or remains the same, never decreasing.

But it was only understood in a statistical sense. Only in systems with large numbers of particles all interacting with one another does this type of chaos typically manifest, driving these dual phenomena of time irreversibility and entropy increases. Of course, the same rules that govern many-particle systems have to govern few-particle systems as well, so there should be examples of chaos, irreversibility, and entropy increases in systems without many particles at all.

By considering the evolution and details of a system with as few as three particles, scientists have been able to show that a fundamental time irreversibility arises in these systems under realistic physical conditions that the Universe is very likely to obey. (NASA/VICTOR TANGERMANN)

In the April 2020 issue of the Monthly Notices of the Royal Astronomical Society, a new paper was published with the title, Gargantuan chaotic gravitational three-body systems and their irreversibility to the Planck length. (Preprint available in full here.) Previous research has shown that chaos in as inherent property of many real-life astrophysical systems, including:

for small, low-mass objects in the Solar System,
systems with only small numbers of stars,
individual star clusters,
and galaxies that evolve with time.

If you have a small, tiny change in the initial conditions of your system — where just one object is in a slightly different location or has a slightly different velocity — you’ll get a completely different result down the road.

The Butterfly Effect, also known as deterministic chaos, is a phenomenon where equations with no uncertainty will still yield uncertain outcomes, no matter how precisely the computations are performed. (PUBLIC DOMAIN)

If you want to understand entropy increase, what you have to look at is the increase in the number of possible outcomes when starting from initial conditions that are only very slightly different from one another. Sometimes, if you vary the initial conditions only slightly, you’ll wind up with the same end state: that’s an example of a converging solution, where entropy doesn’t significantly increase.

But other times, you’ll wind up with very different end states: end states that appear to bear very little relation to what you started off with initially. Those are diverging solutions, and that’s where entropy increase comes from. Although physical systems with large numbers of particles can arrive at this, it’s important to connect them, physically, to the initial conditions that you start off with. This is harder to do for systems with larger numbers of particles, and has been a controversial area of study for the past few decades.

Two systems starting from an identical configuration, but with imperceptibly small differences in initial conditions (smaller than a single atom), will keep to the same behavior for a while, but over time, chaos will cause them to diverge. After enough time have gone by, their behavior will appear completely unrelated to one another. (LARRY BRADLEY)

Recently, however, advances in computing power and brute-force algorithms have enabled certain very simple problems to be solved numerically, and to determine things like:

which problems-and-conditions converge and which ones diverge,
where everything can be calculated to arbitrary precision (at the expense of computing time),
and where, if the solution is time-reversible, you can start at the end state and can retrieve the initial conditions to many digits of precision for every body in the system.

What the new paper by Boekholt, Portegies Zwart, and Valtonen did was to analyze a system of three equal mass, non-rotating black holes (i.e., point masses) that start off at rest but with arbitrary positions. Some solutions to this setup were previously known to be reversible, while others were thought to be irreversible.

This six-panel graphic illustrates a scenario for Eta Carinae’s 1843 outburst where a triple-star system has one member enter the giant phase, loses its outer layers to its nearest companion, which drives the donor star farther away, kicking the outer companion inwards, causing an eventual merger that led to the supernova impostor event. Three body interactions often, but not always, eject one member and wind up with the other two more tightly bound. (NASA, ESA, AND A. FEILD (STSCI))

This new work really does take our understanding to the next level. As you increase the precision of your calculation, taking smaller and smaller steps and increasing your numerical accuracy, more and more of the solutions that appeared irreversible actually turned out to be reversible. The more precisely (i.e., the more significant digits) you calculated the distance between any two objects to be, the better time-reversibility began to look.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

But there’s a limit to this: the limit set by the quantum rules that govern our Universe. You can’t compute distances to arbitrary accuracy in our physical reality because below a certain distance scale — the Planck scale, or around 10^-35 meters — the laws of physics break down. By considering black holes with masses of ~1 million solar masses and initial separations on the order of ~1 light-year, they find that about 5% of all configurations are fundamentally irreversible.

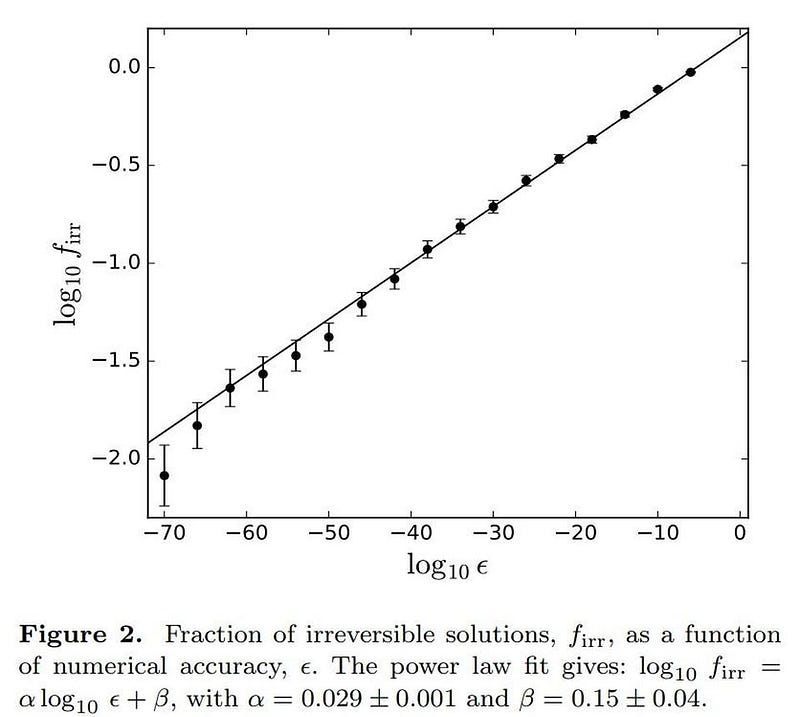
Two parameters that help in the calculation of reversibility, with the x-axis parameter corresponding to the smallness of the steps taken to successfully evolve the problem. At some point, for any system, cutting off the simulation’s size (to correspond to the minimum physical distance length) renders a fraction of these problems fundamentally irreversible. (T.C.N. BOEKHOLT, S.F. PORTEGIES ZWART AND M. VALTONEN, MNRAS 493, 3 (2020))

It’s a very clever result to learn that, for the realistically large-mass objects we have in our Universe, the precision required to calculate a truly rime-reversible solution is greater than the precision the physical Universe actually allows. If the laws of quantum physics and General Relativity are both correct, as we have every reason to believe that they are, then even purely gravitational systems with as few as three masses are fundamentally irreversible.

Of course, plenty of other reactions are known to be irreversible as well: two orbiting black holes emit gravitational radiation and inspiral, but no orbiting black holes absorb gravitational radiation and outspiral, for example. But for the first time, scientists have demonstrated — assuming the laws of physics are what we think they are — that a purely classical system with only three masses isn’t always time-reversible. The Universe really is unpredictable and chaotic at a fundamental level.

Send in your Ask Ethan questions to startswithabang at gmail dot com!

Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.