Ask Ethan: Why Are There Only Three Generations Of Particles?

With the discovery of the Higgs boson, the Standard Model is now complete. Can we be sure there isn’t another generation of particles out there?
The Universe, at a fundamental level, is made up of just a few different types of particles and fields that exist amidst the spacetime fabric that composes otherwise empty space. While there may be a few components of the Universe that we don’t understand — like dark matter and dark energy — the normal matter and radiation not only well-understood, it’s perfectly well-described by our best theory of particles and their interactions: the Standard Model. There’s an intricate but ordered structure to the Standard Model, with three “generations” of particles. Why three? That’s what Peter Brouwer wants to know, asking:
Particle families appear as a set of 3, characterised by the electron, muon and tau families. The last 2 being unstable and decaying. So my question is: Is it possible that higher order particles exist? And if so, what energies might such particles be found? If not, how do we know that they don’t exist.
This is a big question. Let’s dive in.
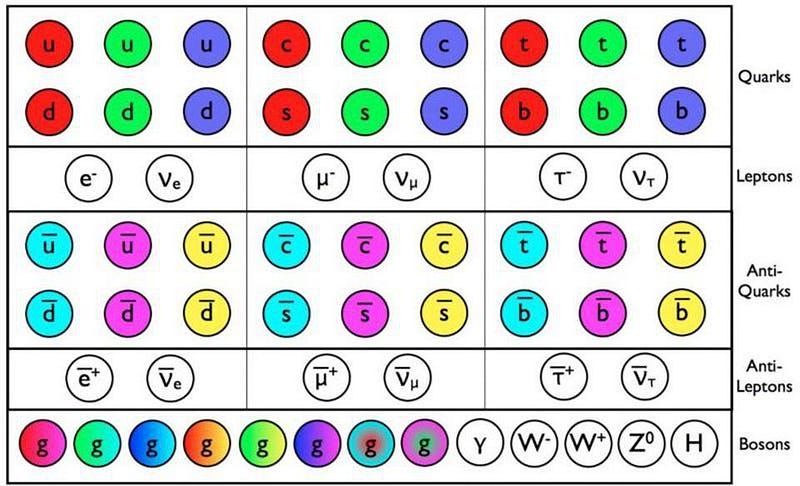
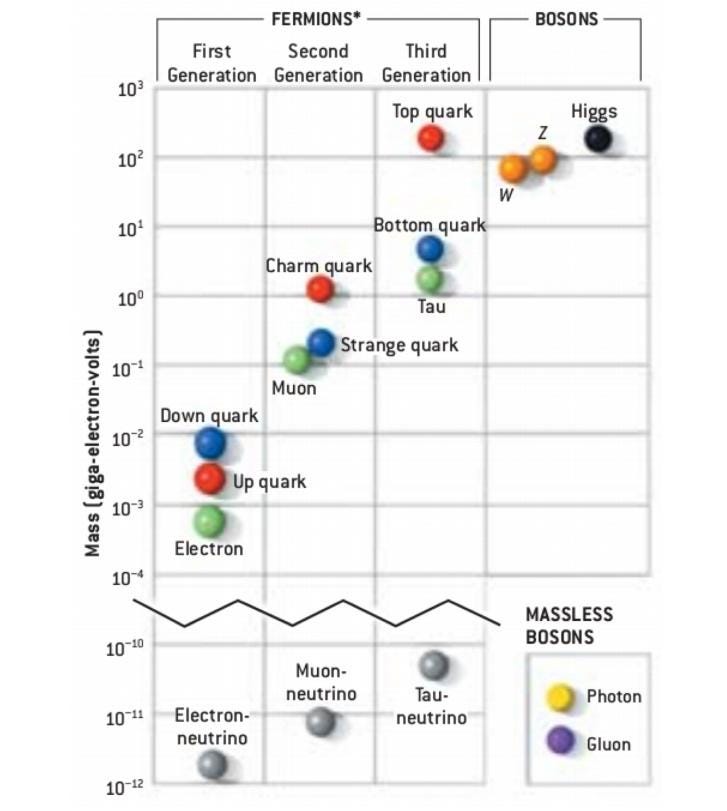
There are two classes of particles in the Standard Model: the fermions, which have half-integer spins (±½, ±1½, ±2½, etc.) and where every fermion has an antimatter (anti-fermion) counterpart, and the bosons, which have integer spins (0, ±1, ±2, etc.) and are neither matter nor antimatter. The bosons simply are what they are: 1 Higgs boson, 1 boson (photon) for the electromagnetic force, 3 bosons (W+, W- and Z) for the weak force, and 8 gluons for the strong force.
The bosons are the force-carrying particles that enable the fermions to interact, but the fermions (and anti-fermions) carry fundamental charges that dictate which forces (and bosons) they’re affected by. While the quarks couple to all three forces, the leptons (and anti-leptons) don’t feel the strong force, and the neutrinos (and anti-neutrinos) don’t feel the electromagnetic force, either.
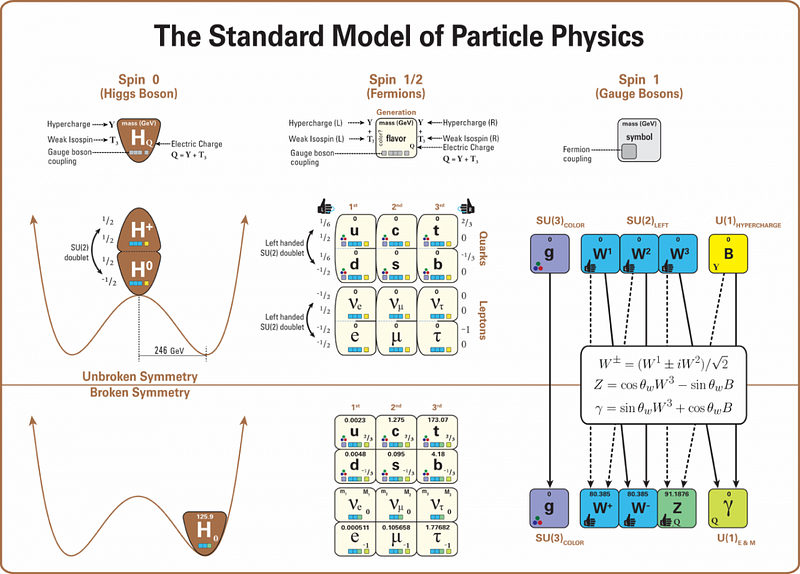
But what’s perhaps most puzzling about the Standard Model is that unlike the bosons, there are “copies” of the fermions. In addition to the fermionic particles that make up the stable or quasi-stable matter we’re familiar with:
- protons and neutrons (made of bound states of up-and-down quarks along with the gluons),
- atoms (made of atomic nuclei, which is made of protons and neutrons, as well as electrons),
- and electron neutrinos and electron antineutrinos (created in the nuclear reactions that involve building up to or decaying down from pre-existing nuclear combinations),
there are two additional generations of heavier particles for each of these. In addition to the up-and-down quarks and antiquarks in 3 colors apiece, there are also the charm-and-strange quarks plus the top-and-bottom quarks. In addition to the electron, the electron neutrino and their antimatter counterparts, there are also the muon and muon neutrino, plus the tau and the tau neutrino.
For some reason, there are three copies, or generations, of fermionic particles that show up in the Standard Model. The heavier versions of these particles don’t spontaneously arise from conventional particle interactions, but will show up at very high energies.
In particle physics, you can create any particle-antiparticle pair at all so long as you have enough available energy at your disposal. How much energy do you need? Whatever the mass of your particle is, you need enough energy to create both it and its partner antiparticle (which happens to always have the same mass as its particle counterpart). From Einstein’s E = mc², which details the conversion between mass and energy, so long as you have enough energy to make them, you can. This is exactly how we create particles of all types from high-energy collisions, like the kind occurring in cosmic rays or at the Large Hadron Collider.
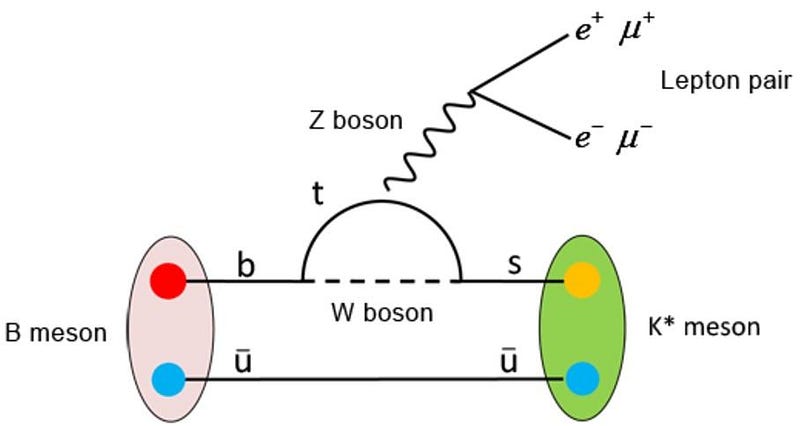
By the same token, whenever you create one of these unstable quarks or leptons (leaving neutrinos and antineutrinos aside), there’s always the possibility that they’ll decay to a lighter particle through the weak interactions. Because all the Standard Model fermions couple to the weak force, it’s only a matter of a fraction-of-a-second before any of the following particles — strange, charm, bottom, or top quarks, as well as the muon or tau leptons — decay down to that stable first generation of particles.
As long as it’s energetically allowed and not forbidden by any of the other quantum rules or symmetries that exist in our Universe, the heavier particles will always decay in this fashion. The big question, though, of why there are three generations, is driven not by theoretical motivations, but by experimental results.

The muon is the lightest of the fermions to extend beyond the first generation of particles, and caused the famed physicist I. I. Rabi to exclaim, when he was shown the evidence of this particle “who ordered that?” As particle accelerators became more ubiquitous and more energetic over the next decades, particles like mesons and baryons, including ones with strange quarks and later charmed quarks, soon surfaced.
However, it was only with the advent of the Mark I experiment at SLAC in the 1970s (which co-discovered the charm quark) that evidence for a third generation arose: in the form of the tau (and anti-tau) lepton. That 1976 discovery is now 43 years old. In the time since, we’ve directly detected every particle in the Standard Model, including all of the quarks and neutrinos and anti-neutrinos. Not only have we found them, but we’ve measured their particle properties exquisitely.
Based on all we now know, we should be able to predict how these particles interact with themselves and one another, how they decay, and how they contribute to things like cross-sections, scattering amplitudes, branching ratios and event rates for any particle we choose to examine.
The structure of the Standard Model is what enables us to do these calculations, and the particle content of the Standard Model enables us to predict which light particles the heavier ones will decay into. Perhaps the strongest example is the Z-boson, the neutral particle that mediates the weak force. The Z-boson is the third most massive particle known, with a rest mass of 91.187 GeV/c²: nearly 100 times more massive than a proton. Every time we create a Z-boson, we can experimentally measure the probability that it will decay into any particular particle or combinations of particles.
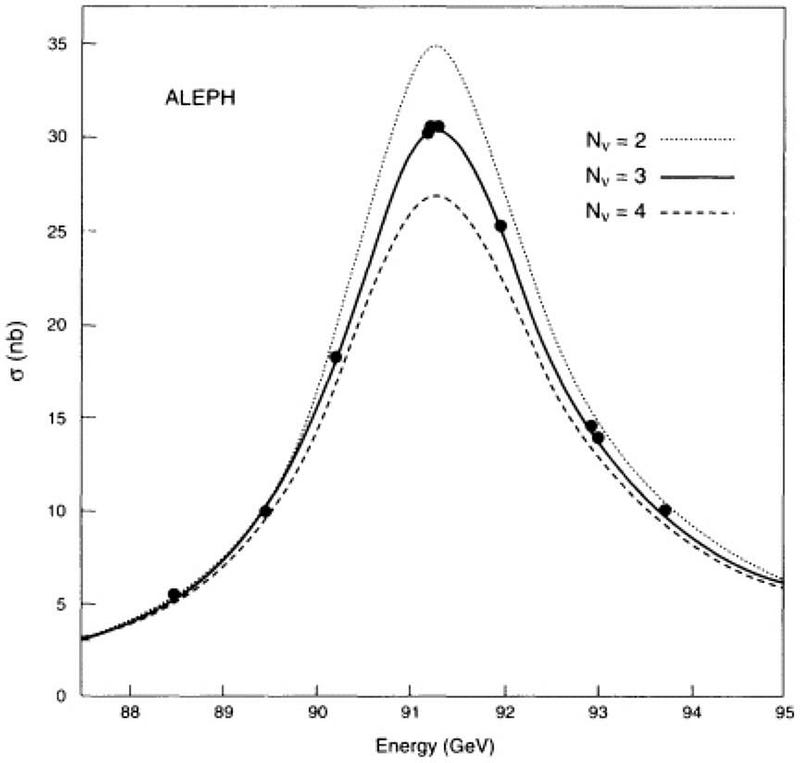
By examining what fraction of the Z-bosons we create in accelerators decay to:
- electron/positron pairs,
- muon/anti-muon pairs,
- tau/anti-tau pairs,
- and “invisible” channels (i.e., neutrinos),
we can determine how many generations of particles there are. As it turns out, 1-out-of-30 Z-bosons decay to each of electron/positron, muon/anti-muon, and tau/anti-tau pairs, while a total out of 1-in-5 Z-boson decays are invisible. According the Standard Model and our theory of particles and their interactions, that translates to 1-in-15 Z-bosons (with ~6.66% odds) will decay to each of the three types of neutrinos that exist.
These results tell us that if there is a fourth (or more) generation of particles, every single one of them, including leptons and neutrinos, have a mass that’s greater than 45 GeV/c²: a threshold that only the Z, W, Higgs, and top particles are known to exceed.
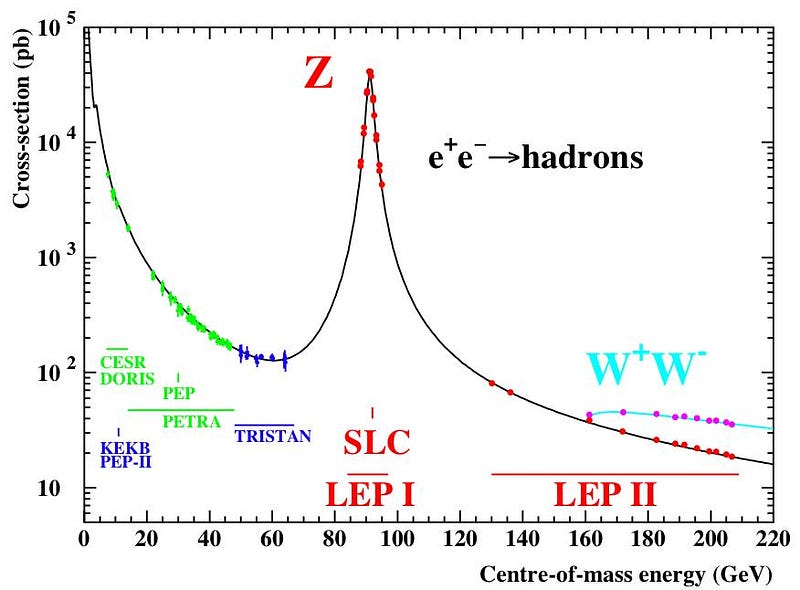
Now, there’s nothing forbidding a fourth generation from existing and being much, much heavier than any of the particles we’ve observed so far; theoretically, it’s very much allowed. But experimentally, these collider results aren’t the only thing constraining the number of generational species in the Universe; there’s another constraint: the abundance of the light elements that were created in the early stages of the Big Bang.
When the Universe was approximately one second old, it contains only protons, neutrons, electrons (and positrons), photons, and neutrinos and anti-neutrinos among the Standard Model particles. Over those first few minutes, protons and neutrons will eventually fuse to form deuterium, helium-3, helium-4, and lithium-7.
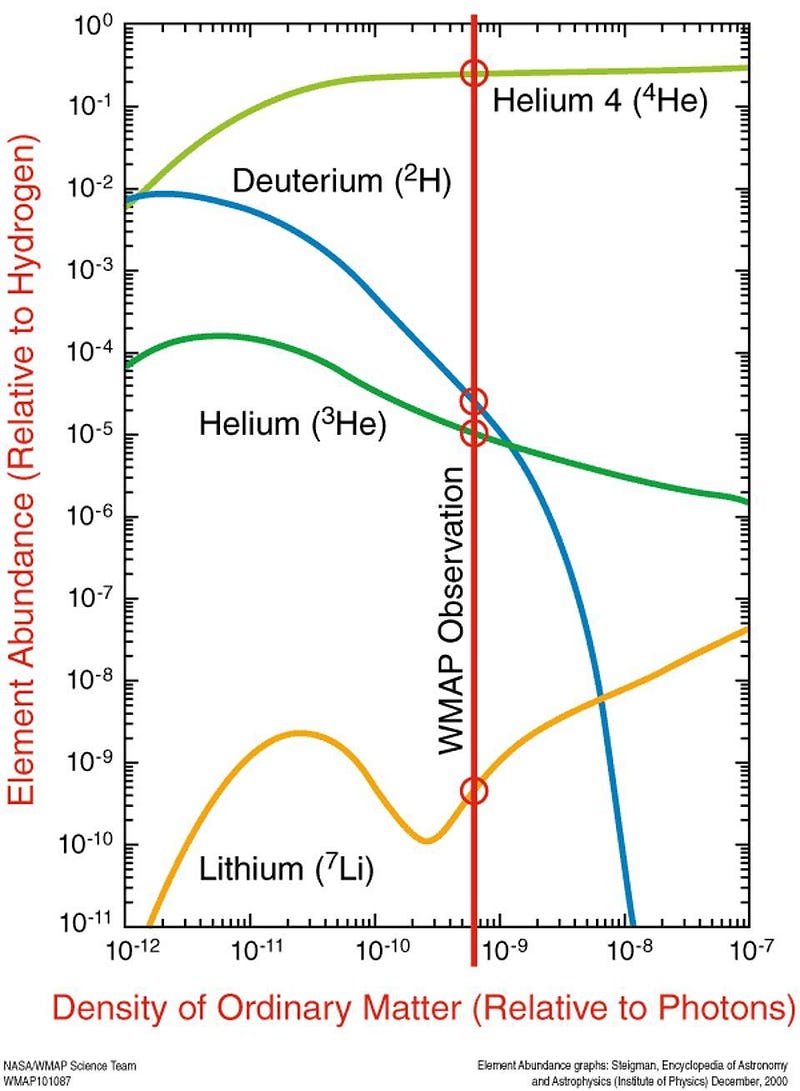
But how much will they form? That’s dependent on just a few parameters, like the baryon-to-photon ratio, which is commonly used to predict these abundances as the only parameter we vary.
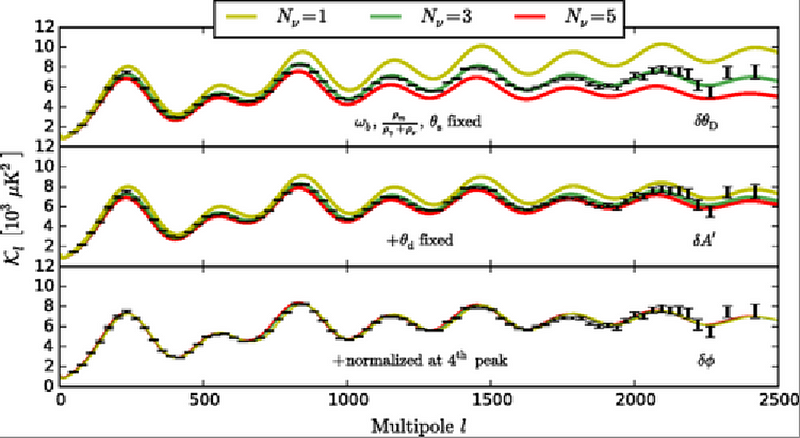
But we can vary any number of parameters we typically assume are fixed, such as the number of neutrino generations. From Big Bang Nucleosynthesis, as well as from the imprint of neutrinos on the leftover radiation glow from the Big Bang (the cosmic microwave background), we can conclude that there are three — not two or fewer and not four or more — generations of particles in the Universe.
It is eminently possible that there are more particles out there than the Standard Model, as we know it, presently predicts. In fact, given all the components of the Universe that aren’t accounted for in the Standard Model, from dark matter to dark energy to inflation to the origin of the matter-antimatter asymmetry, it’s practically unreasonable to conclude that there aren’t additional particles.
But if the additional particles fit into the structure of the Standard Model as an additional generation, there are tremendous constraints. They could not have been created in great abundance during the early Universe. None of them can be less massive than 45.6 GeV/c². And they could not imprint an observable signature on the cosmic microwave background or in the abundance of the light elements.
Experimental results are the way we learn about the Universe, but the way those results fit into our most successful theoretical frameworks is how we conclude what else does and doesn’t exist in our Universe. Unless a future accelerator result surprises us tremendously, three generations is all we get: no more, no less, and nobody knows why.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.