Ask Ethan: When Do Black Holes Become Unstable?

The densest objects in the Universe are also the most difficult to destroy. But eventually, destruction always prevails.
There are quite a few ways to make the black holes we know about in the Universe, from core-collapse supernovae to merging neutron stars to the direct collapse of tremendous amounts of matter. On the smallest end, we know of black holes that may be merely 2.5-to-3 times the mass of our Sun, while on the largest end, supermassive ones in excess of 10 billion solar masses reside at the centers of galaxies. But is that it? And how stable are black holes of different masses? That’s what Nyccolas Emanuel wants to know, as he asks:
Is there a critical size for black hole stability? [A] 10¹² kg [black hole] is already stable for a couple of billion years. However, a [black hole] in the range of 10⁵ kg, could explode in a second, thus, definitely not stable… I guess there is a critical mass for a [black hole] where the flow of gained matter will equal to the Hawking evaporation?
There’s a lot going on here, so let’s unpack it all.
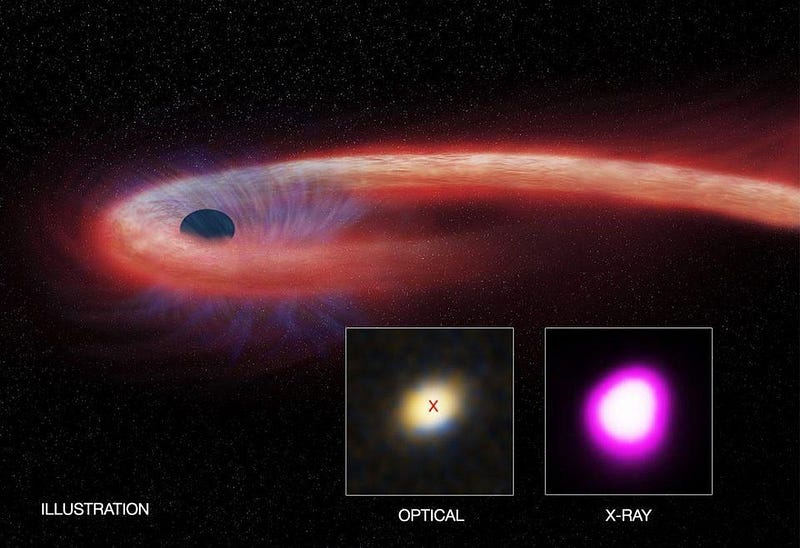
The first thing to start with is the stability of a black hole itself. For any other object in the Universe, astrophysical or otherwise, there are forces that hold it together against whatever the Universe might do to try and tear it apart. A hydrogen atom is a tenuously held-together structure; a single ultraviolet photon can destroy it by ionizing its electron. An atomic nucleus needs a much higher-energy particle to blast it apart, like a cosmic ray, an accelerated proton, or a gamma-ray photon.
But for larger structures, like planets, stars or even galaxies, the gravitational forces holding them together are enormous. Normally, it takes either a runaway fusion reaction or an incredibly strong, external gravitational pull — such as from a passing star, black hole, or galaxy — to tear such a megastructure apart.

For black holes, however, something is fundamentally different. Rather than their mass being distributed over a volume, it’s compressed down into a singularity. For a non-rotating black hole, that’s just a single, zero-dimensional point. (For rotating ones, it’s not much better: an infinitely-thin, one-dimensional ring.)
Furthermore, all of the mass-and-energy-containing contents of a black hole are contained within an event horizon. Black holes are the only objects in the Universe that contain an event horizon: a boundary where, if you slip within it, it’s impossible to escape. No acceleration, and hence no force, no matter how strong, will ever be able to pull matter, mass, or energy from inside the event horizon outside to the Universe beyond.

This might imply that black holes, once you form one via any means possible, can only grow, and never be destroyed. In fact, they do grow, and relentlessly at that. We observe all sorts of phenomena in the Universe, such as:
- quasars,
- blazars,
- active galactic nuclei,
- microquasars,
- stars orbiting large masses that emit no light of any type,
- and flaring, X-ray and radio emissions from galactic centers,
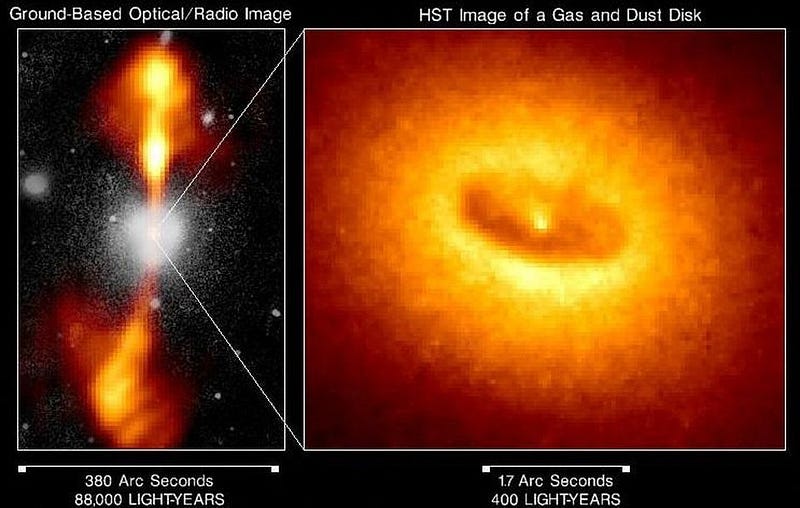
that are all thought to be driven by black holes. By inferring their masses, we can thereby know the physical sizes of their event horizons. Anything that collides with it, crosses over into it, or even grazes it will inevitably fall inside. And then, by the conservation of energy, it must inevitably increase the black hole’s mass.

This is a process that, on average, is happening for every black hole in the Universe known today. Material from other stars, from cosmic dust, from interstellar matter, gas clouds, or even the radiation and neutrinos left over from the Big Bang can all contribute. Intervening dark matter will collide with the black hole, increasing its mass as well. All told, black holes grow depending on the matter-and-energy density surrounding them; the monster at the center of our Milky Way grows at a rate of about one solar mass every 3,000 years; the black hole at the center of the Sombrero galaxy grows at a rate of one solar mass every two decades.
The larger and heavier your black hole is, on average, the faster it grows, dependent on the other material it encounters. As time goes on, the rate-of-growth will drop, but with a Universe that’s only about 13.8 billion years old, they continue to grow prodigiously.

On the other hand, black holes aren’t just growing over time; there’s also a process by which they evaporate: Hawking radiation. This was the topic of last week’s Ask Ethan, and is due to the fact that space is severely curved close to the event horizon of a black hole, but flatter farther away. If you are an observer a great distance away, you’ll see a non-negligible amount of radiation being emitted from the curved region near the event horizon, owing to the fact that the quantum vacuum has different properties in differently-curved regions of space.
The net result is that black holes wind up emitting thermal, blackbody radiation (mostly in the form of photons) in all directions around it, over a volume of space that mostly encapsulates approximately ten Schwarzschild radii of the location of the black hole. And, perhaps counterintuitively, the less massive your black hole is, the faster it evaporates.

Hawking radiation is an incredibly slow process, where a black hole the mass of our Sun would take 10⁶⁴ years to evaporate; the one at the Milky Way’s center would require 10⁸⁷ years, and the most massive ones in the Universe could take up to 10¹⁰⁰ years. In general a simple formula you can use to calculate the evaporation time for a black hole is to take the timescale for our Sun and multiply it by:
(Mass of the black hole/Mass of the Sun)³,
which means that a black hole of the Earth’s mass would survive 10⁴⁷ years; one the mass of the Great Pyramid at Giza (~6 million tons) would remain for about a thousand years; one the mass of the Empire State building would last for about a month; one the mass of an average human would last just under a picosecond. As your mass decreases, you evaporate more quickly.

For all that we know, the Universe could contain black holes of an extraordinarily wide range of masses. If it were born with light ones — anything below about a billion tons — those would all have evaporated by the present day. There is no evidence of black holes that are heavier than that until you get to the ones created by neutron star-neutron star mergers, which begin to arise at about 2.5 solar masses in theory. Above that, X-ray studies point to the existence of black holes in the range of ~10-to-20 solar masses; LIGO has shown us black holes ranging from 8 up to approximately 62 solar masses; and astronomy studies reveal the supermassive black holes that are found throughout the Universe.
There’s a wide range of black holes that we know of, but also a wide range of studies that rule out black holes composing a majority of the dark matter over a huge variety of regimes.
Today, all the black holes that actually, physically exist are gaining matter at a far greater rate than Hawking radiation is causing them to lose mass. For a solar-mass black hole, it loses about 10^-28 Joules of energy every second. Considering that:
- even a single photon from the Cosmic Microwave Background has about a million times that energy,
- there are about 411 such photons (left over from the Big Bang) per cubic centimeter of space,
- and they move at the speed of light, meaning approximately 10 trillion photons-per-second collide with every square-centimeter of area an object takes up,
even an isolated black hole in the depths of intergalactic space would have to wait until the Universe was around 10²⁰ years old — more than a billion times its current age — before the rate of black hole growth drops below the rate of Hawking radiation.
But let’s play the game. Assuming you lived in intergalactic space, away from all normal matter and dark matter, away from all cosmic rays and stellar radiation and neutrinos, and only had the photons left over from the Big Bang to contend with. How big would your black hole need to be so that the rate of Hawking radiation (evaporation) and the rate of photon absorption by your black hole (growth) balanced each other?
The answer comes out to around 10²³ kg, or approximately the mass of the planet Mercury. If it were a black hole, Mercury would be approximately a half-a-millimeter in diameter, and would radiate approximately 100 trillion times as quickly as a solar mass black hole. That’s the mass, in the Universe today, that it would take for a black hole to absorb as much Cosmic Microwave Background radiation as it would emit in Hawking radiation.

For a realistic black hole, you cannot isolate it from the remaining matter in the Universe. Black holes, even if they get ejected from galaxies, still fly through the intergalactic medium, encountering cosmic rays, starlight, neutrinos, dark matter, and all sorts of other particles, both massive and massless. The cosmic microwave background is unavoidable no matter where you go. If you’re a black hole, you’re constantly absorbing matter-and-energy, and growing in both mass and size as a result. Yes, you radiate energy away, too, in the form of Hawking radiation, but for all black holes that actually exist in our Universe, it will take at least 100 quintillion years for the rate-of-growth to drop below the rate of radiation, and much, much longer for them to finally evaporate away.
Black holes will eventually become unstable and disappear into nothing but radiation, but unless we create a very low-mass one, somehow, nothing else in the Universe will be around to witness them when they go.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.




