Ask Ethan: When Did The Universe Get Its First Quantum Fields?

Have we always had quantum fields in the Universe? Or did they emerge at some finite time?

No matter how we look at the Universe — at low temperatures or ultra-high energies, from our own backyard to the most distant recesses of the observable cosmos — we find that the same laws of physics apply. The fundamental constants remain the same; gravitation appears to behave the same; the quantum transitions and relativistic effects are identical. At all points in time, at least for the parts of the Universe we can observe, General Relativity (governing gravity) and Quantum Field Theory (governing the other known forces) appear to apply in the exact same form we find them appearing here on Earth. But has it always been this way? Is there a time where the Universe didn’t have the same quantum fields in it, or perhaps no quantum fields at all? That’s what Patreon supporter Chris Shaw wants to know, asking:

“When did the first quantum fields form in the universe? Have they been there since the Big Bang or even from the inflationary period before?”

Perhaps surprisingly, quantum fields are there even under conditions where you might not expect them. Here’s what we know so far.

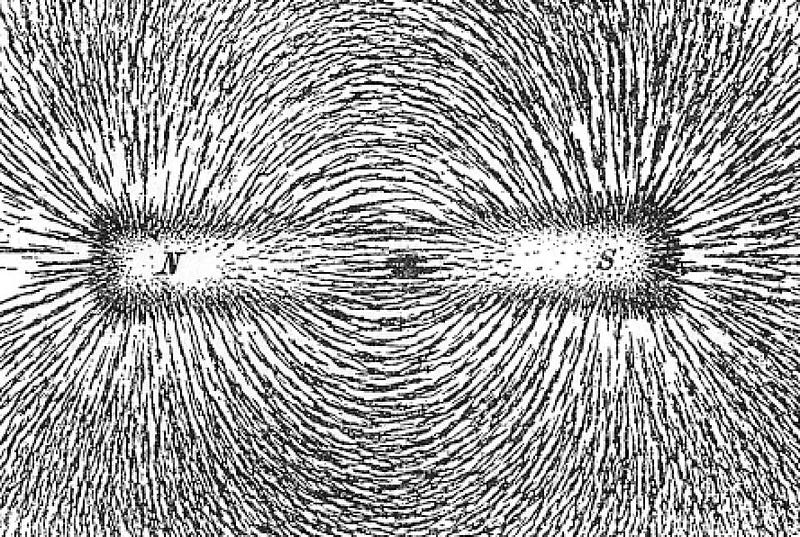
Magnetic field lines, as illustrated by a bar magnet: a magnetic dipole, with a north and south pole bound together. These permanent magnets remain magnetized even after any external magnetic fields are taken away. If you ‘snap’ a bar magnet in two, it won’t create an isolated north and south pole, but rather two new magnets, each with their own north and south poles. Mesons ‘snap’ in a similar manner. (NEWTON HENRY BLACK, HARVEY N. DAVIS (1913) PRACTICAL PHYSICS)

When we think about fields, most of us conceive of them the same way scientists did back in the 1800s: when you have some type of source — like an electric charge or a permanent magnet — it creates a field around it at every point in space. That field exists whether or not there are other particles there to be affected by it, but you can detect the presence of that field (as well as what it affects and how) by observing what happens to charges of various types that interact with that field.

Iron filings, which themselves can get magnetized, respond to magnetic fields by aligning along the direction of a field. Electric charges, in the presence of an electric field (or in motion in the presence of a magnetic field), will experience a force that accelerates them dependent on the strength of the field.

Even gravitation, whether in Einstein’s or Newton’s conception, can be visualized as a field: where matter or energy of any form will respond to the cumulative gravitational effects at its location in space, determining its future trajectory.

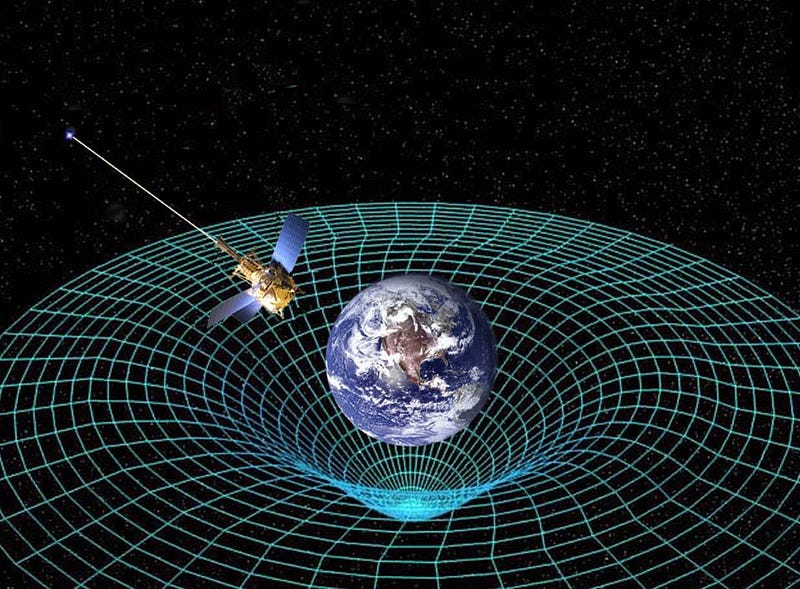
The gravitational field, or the gravitational influence of all objects combined on a region of space in the Universe, can be modeled in any particular frame of reference in both Newton’s and Einstein’s conception of gravity. The concept of a field is extraordinarily useful, but incomplete, in the classical world alone. (NASA)

This visualization, as useful and common as it might be, only works in non-quantum settings, however. It’s an excellent illustration of how classical fields work, but we live in a fundamentally quantum reality. What we conceive of in the classical world — that fields are smooth, continuous, and that its properties can exist anywhere along a spectrum from a theoretical minimum to a theoretical maximum — no longer applies in a quantum Universe.

Instead, a quantum field isn’t only present where you have a source (like a mass or a charge), but rather is omnipresent: everywhere. If you have charges present, such as:

masses (for gravity),
electric charges (for electromagnetism),
a particle with a nonzero weak hypercharge (for the weak nuclear force),
or a color charge (for the strong nuclear force),

they behave like an excited state of the field, but the field is present regardless of the presence or absence of charges. What’s more: the field is quantized, and its zero-point energy, or the lowest energy level it can occupy, is allowed to have non-zero values.

Today, Feynman diagrams are used in calculating every fundamental interaction spanning the strong, weak, and electromagnetic forces, including in high-energy and low-temperature/condensed conditions. Even in the absence of particles, Feynman diagrams exist, and represent the vacuum contribution of quantum fields. (DE CARVALHO, VANUILDO S. ET AL. NUCL.PHYS. B875 (2013) 738–756)

In other words, “empty space” as we understand it, with no charges, masses, or other sources of the field in it, isn’t exactly empty, but still has these quantum fields present within it. That means that quantum fluctuations, which arise as a consequence of the quantum nature of these fields combined with Heisenberg’s uncertainty principle, exist throughout all of space as well, occupying every possible quantum mode and state (with specific, and in-principle computable, probabilities for those states to be occupied) allowable by the system.

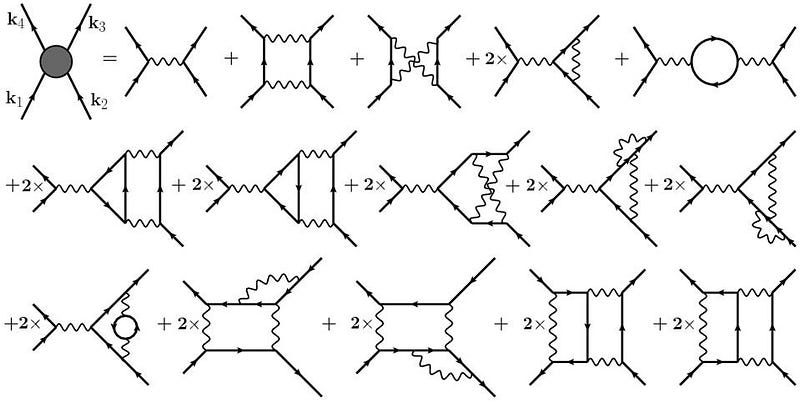
You might be skeptical of this approach, thinking to yourself something along the lines of, “well, so what? Quantum field theory is just one approach to doing calculations; it’s not like there’s an experimental test of whether these quantum fields exist in the reality of empty space or not.” But there is a test. You can take two parallel, conducting plates, and place them in the most perfect vacuum you can create: where there’s no matter and no sources of any type, just the quantum fields inherent to empty space, including the fundamental quantum electromagnetic field.

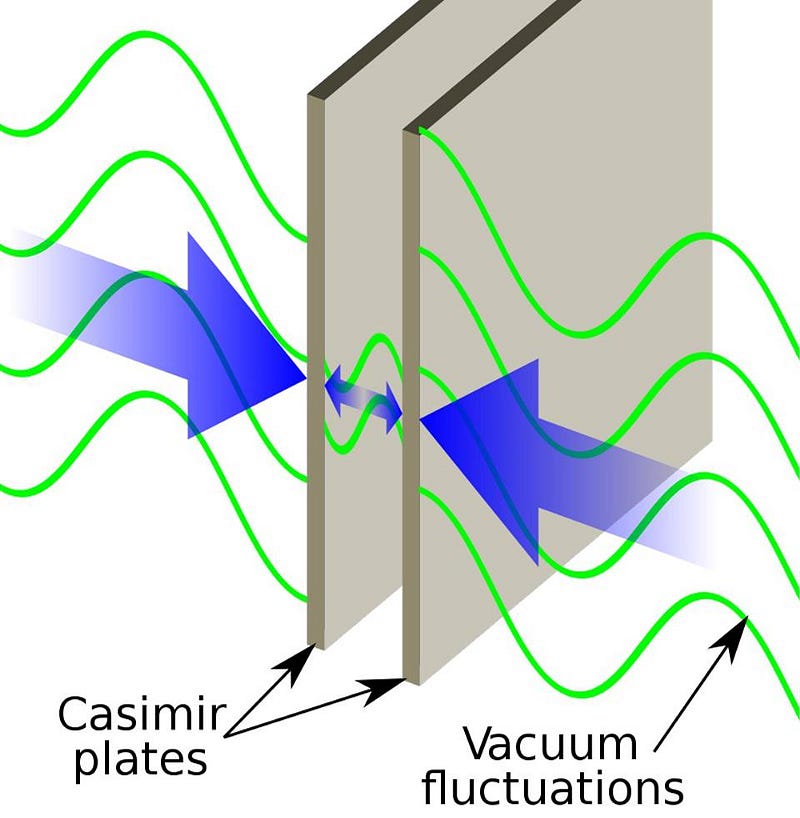
An illustration of the Casimir effect, and how the forces (and allowed/forbidden states of the electromagnetic field) on the outside of the plates are different from the forces on the inside. This results in a net attractive force, as more quantum modes are allowed outside than inside the plates. (EMOK / WIKIMEDIA COMMONS)

Outside of those two plates, all of the possible states of these quantum fields are allowed, as there are no restrictions on which modes are forbidden. But inside those plates, only a subset of those quantum fields are allowed, as there are boundary conditions that prevent certain electromagnetic waves — and hence, certain excitations of the quantum fields — from existing. Even without any sources for those electromagnetic waves, those excited field states (or, if it makes it easier for you to visualize it, those virtual modes and particles) are different inside and outside those plates, creating a net force on those plates: the Casimir force.

Predicted by scientist Hendrik Casimir back in 1948, the first experimental detection of this force didn’t occur until 1997, when physicist Steve Lamoreaux accomplished the feat and got a result that was within 5% of Casimir’s predicted value for the system. These quantum fields really do exist all throughout space, and experiments not only show that they do exist, but show us the magnitude of their effects as well.

The contributions of the known quantum fields to the vacuum cannot be practically calculated today, but can be calculated in principle if we had an arbitrary amount of computational power. It is unknown whether the known fields, particles, and interactions are sufficient to account for the Universe we experience today, or if there are additional ones we have yet to detect. (DEREK LEINWEBER)

One of the concepts that physicists wonder about is whether the quantum fields we know about — the ones that are a part of the Standard Model plus whatever the (assumed) quantum fields associated with gravity are — make up all of the quantum fields permeating empty space, or whether there are others. For example, could there be additional quantum fields arising from:

whatever is responsible for dark matter,
whatever phenomenon or field causes dark energy,
any fields left over from the Universe’s inflationary phase,
new fields or interactions arising from some sort of grand unification,
or any other exotic new physics (including, but not limited to, new forces or particles) that may exist beyond the Standard Model.

Although the laws of physics don’t change over the conditions we’ve observed them, from here to particle accelerators to the earliest observable stages of the Big Bang, the properties of quantum fields ensure that the strength of quantum couplings, corresponding to the forces experienced by particles owing to these quantum fields, actually change as a function of energy and temperature.

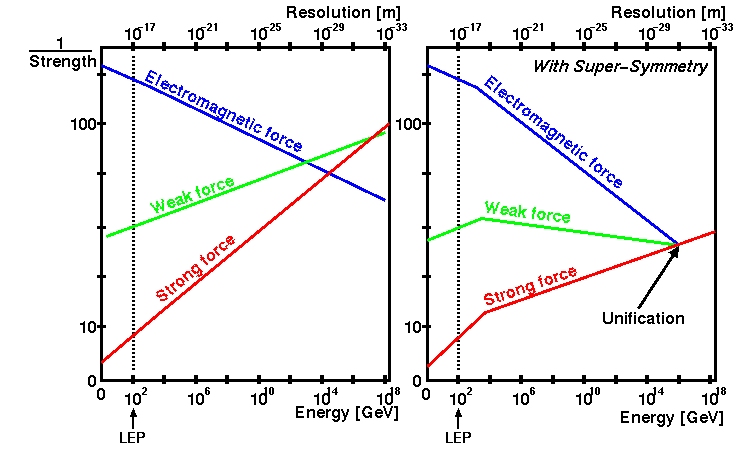
When you view the coupling constants as a function of energy on a log-log scale, they appear to nearly miss one another, at left. If you add in the supersymmetric particles as predicted, the constants meet (or come much closer to meeting) at ~1⁰¹⁵ GeV, or the traditional grand unification scale. (CERN (EUROPEAN ORGANIZATION FOR NUCLEAR RESEARCH), 2001)

In physics, we call this “the running of the coupling constants,” and you can visualize it as having more excited-state modes occupied by these virtual quantum particles as compared to greater fractions of lower-energy, ground-state modes. Although this doesn’t imply that the quantum fields that govern the Universe were different at earlier, higher-energy times, it is suggestive of something: that perhaps these coupling constants unify at some point, indicating that the strong, weak, and electromagnetic forces might have arisen from a grander theory where all the forces are unified.

That framework not only offers up the possibility that additional quantum fields might show up and reveal their effects at those high energies, but that there might be some sort of “ultimate unification,” or a theory of everything. If such a state exists, you can imagine that as the ultimate version of a restored symmetry: like putting a ball at the absolute top of the highest mountain peak on a planet.

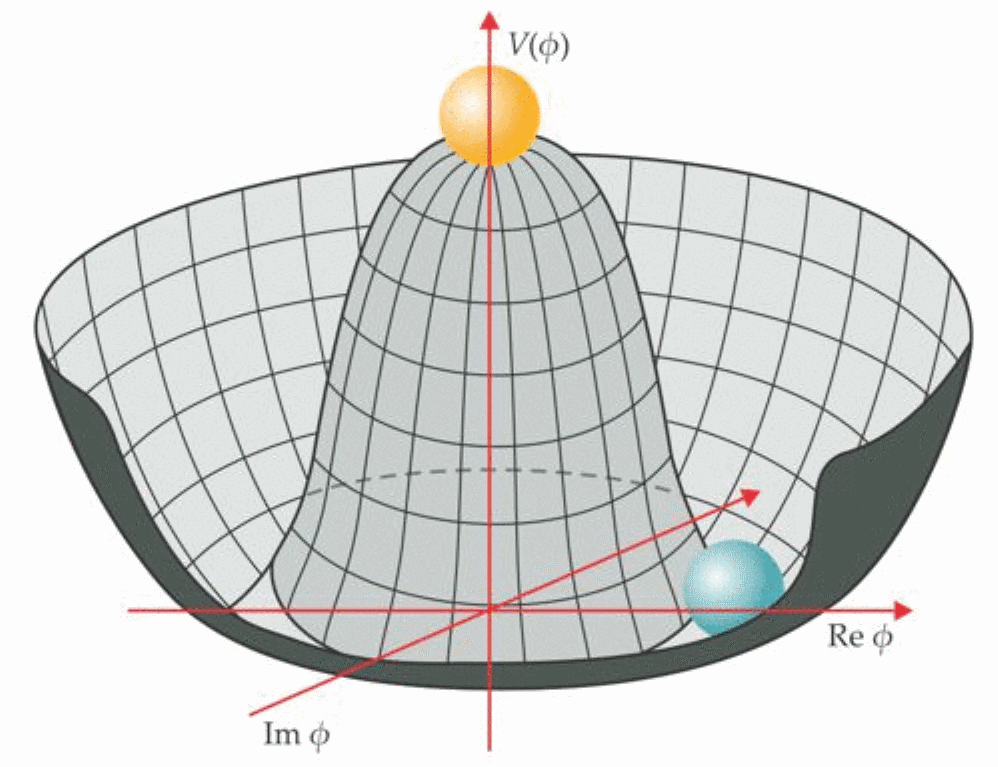
When a symmetry is restored (yellow ball at the top), everything is symmetric, and there is no preferred state. When the symmetry is broken at lower energies (blue ball, bottom), the same freedom, of all directions being the same, is no longer present. It’s eminently possible that there are multiple “low points” that the ball could roll into for any quantum field imaginable. (PHYS. TODAY 66, 12, 28 (2013))

When a symmetry breaks, that’s like rolling down the hill and into the lowest point of whatever valley it happens to fall into. But if you bring the ball back up to the top of the hill multiple times and balance it as best as you can, it won’t necessarily roll down the same way every time. Depending on factors like:

very slight differences in initial conditions,
small, even quantum, fluctuations,
at what rate the Universe expands or cools,
and the presence or absence of novel field couplings,

that broken symmetry can wind up in one of any number of possible final states. There is no guarantee, if we ran the clock back to some extremely early time, the laws of physics and the fundamental constants that emerged to govern our Universe would be the same each and every time we did it. Just like we believe we “won” the cosmic lottery by having human life arise on Earth (and most probably nowhere else in the Universe), it’s possible we won the cosmic lottery by getting the laws and constants that we did.

An illustration of multiple, independent Universes, causally disconnected from one another in an ever-expanding cosmic ocean, is one depiction of the multiverse idea. Different “pocket Universes” can arise in a multiverse, but no one knows if these universes will have different laws or fundamental constants from our own. (OZYTIVE / PUBLIC DOMAIN)

When we run the clock backwards to the earliest stages of the hot Big Bang, however, we see no evidence that the Universe ever reached sufficient temperatures that this theorized unification (and restoration of a symmetry) actually occurred. When you break a symmetry, particles are produced, and if this type of grand unification occurred, it should have produced a large number of magnetic monopoles: particles that clearly don’t exist in our Universe. If the quantum fields that we know of today emerged from some earlier state where they didn’t exist previously, that state must be confined to a realm before the hot Big Bang.

Does that mean they could have been created during cosmic inflation?

It’s possible, but we don’t know. Based on the inferred limits on the energies achieved during inflation — which themselves come from the fluctuations generated during inflation that are imprinted in our CMB and large-scale structure today — inflation might not have reached sufficient energies for this to occur. Although successful models of inflation demand a multiverse, it’s still speculative to presume that the constants or laws are different in different “pocket Universes.”

The quantum fluctuations that occur during inflation do indeed get stretched across the Universe, but they also cause fluctuations in the total energy density. These field fluctuations cause density imperfections in the early Universe, which then lead to the temperature fluctuations we experience in the cosmic microwave background. The fluctuations, according to inflation, must be adiabatic in nature. (E. SIEGEL / BEYOND THE GALAXY)

However, one thing that is certain is that quantum fields of some variety must have still existed during inflation. They may or may not be the same quantum fields that exist today, and there may have been additional quantum fields over and above the ones we know of and have today, but they had to exist. How do we know? Because the fluctuations that we see in the Universe, the ones that gave rise to the cosmic structure that eventually formed, match exactly the ones predicted to arise from fluctuating quantum fields that existed during inflation.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

Those fluctuations, the ones that normally occur on tiny, microscopic quantum scales, get stretched across the Universe during inflation, get translated into temperature and density fluctuations at the start of the hot Big Bang, and imprint themselves irrevocably onto the Universe. The fact that we’ve observed these fluctuations and their consequences tell us, quite definitively, that those quantum fields did exist during inflation.

For as long as spacetime has existed, some version of quantum fields must have existed as well. But whatever occurred in our Universe prior to the final tiny fraction-of-a-second of inflation can never be observed or accessed from within our observable Universe. In the absence of evidence, we are bound to probe the limits of what’s known and match them up with whatever’s left as a possibility. However fun and instructive it may be to speculate, the truth is we simply don’t know.

Send in your Ask Ethan questions to startswithabang at gmail dot com!

Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.