Ask Ethan: If Mass Curves Spacetime, How Does It Un-Curve Again?

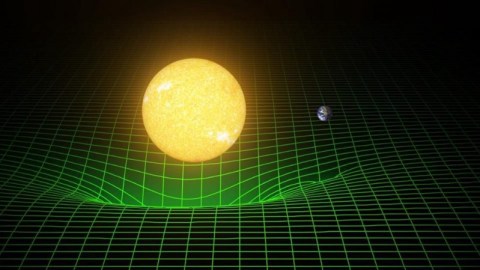
If spacetime is like a fabric, and mass bends it, what flattens it back out again?

Matter tells space how to curve, and curved space tells matter how to move. That’s the basic principle behind Einstein’s General Relativity, which linked, for the first time, the phenomenon of gravity with that of spacetime and relativity. Place a mass down anywhere in the Universe, and the space around it will curve in response. But if you take that mass away, or move it elsewhere, what causes the spacetime to “snap back” to its unbent position? That’s the Ask Ethan question of Edgar Carpenter, who writes:

We are taught that mass warps spacetime, and the curvature of spacetime around mass explains gravity — so that an object in orbit around Earth, for example, is actually going in a straight line through curved spacetime. Ok, that makes sense, but when mass (like the Earth) moves through spacetime and bends it, why does spacetime not stay bent? What mechanism un-warps that area of spacetime as the mass moves on?

There’s a lot that’s interesting about this question, and the answer is one that can really help you to understand how gravity actually works.

The curvature of space, as induced by the planets and Sun in our Solar System, must be taken into account for any observations that a spacecraft or other observatory would make. General Relativity’s effects, even the subtle ones, cannot be ignored. (NASA/JPL-Caltech, for the Cassini mission)

For hundreds of years prior to Einstein, our best gravitational theory came from Newton. Newton’s concept of the Universe was simple, straightforward, and philosophically dissatisfying to many. He claimed that any two masses in the Universe, no matter where they were located or how far apart they were, would instantaneously attract one another via a mutual force known as gravity. The more massive each mass was, the greater the force, and farther away they were (squared), the lesser the force. This would apply to all objects in the Universe, and Newton’s Law of Universal Gravitation, unlike all the other alternatives put forth, agreed with observations precisely.

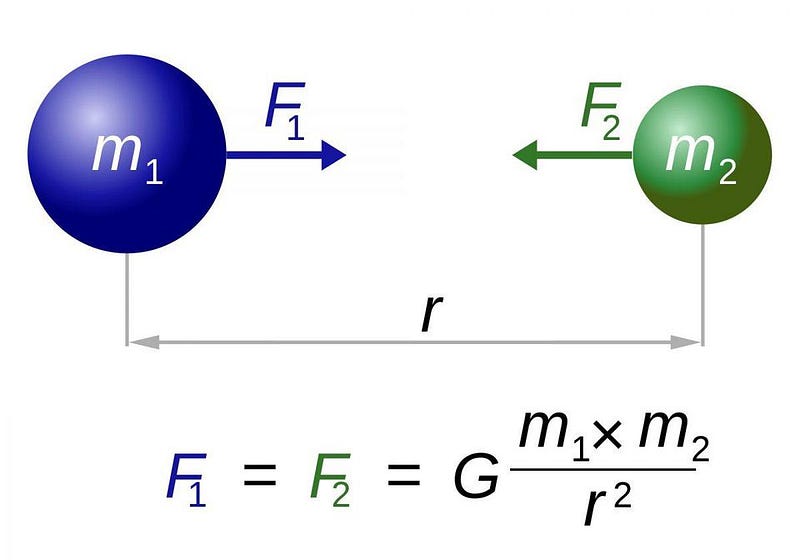
*Newton’s law of Universal Gravitation has been superseded by Einstein’s general relativity, but relied on the concept of an instantaneous action (force) at a distance.* (Wikimedia commons user Dennis Nilsson)

But it introduced an idea that many top intellectuals of the day could not accept: the concept of action-at-a-distance. How could two objects located half-a-Universe away suddenly and instantly exert a force on one another? How could they interact from so far away without anything intervening to mediate it? Descartes couldn’t accept it, and instead formulated an alternative where there was a medium that gravity traveled through. Space is filled with a type of matter, he argued, and that as a mass moved through it, it displaced that matter and created vortices: an early version of the aether. This was the earliest in a long line of what would be called mechanical (or kinetic) theories of gravity.

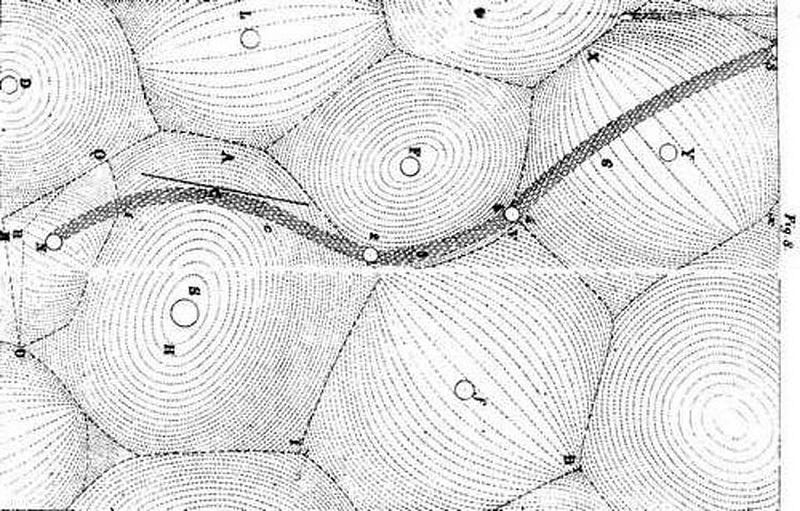
In Descartes’ vision of gravity, there was an aether permeating space, and only the displacement of matter through it could explain gravitation. This did not lead to an accurate formulation of gravity that matched with observations. (René Descartes: Prinzipien der Philosophie, Teil 3)

Descartes’ conception, of course, was wrong. Agreement with experiment is what determines the utility of a physical theory, not our predispositions towards certain aesthetic criteria. When General Relativity came along, it changed the picture Newton’s laws had painted for us in some fundamental ways. For example:

Space and time were not absolute and the same everywhere, but were related and behaved differently for observers moving at different speeds and at different locations.
Gravitation isn’t instantaneous, but only travels at a limiting speed: the speed of light.
And that gravitation isn’t determined by mass and position directly, but by the curvature of space, which itself is determined by the full suite of matter and energy throughout the Universe.

Action-at-a-distance was here to stay, but Newton’s “infinite-range force through static space” was replaced by spacetime curvature.

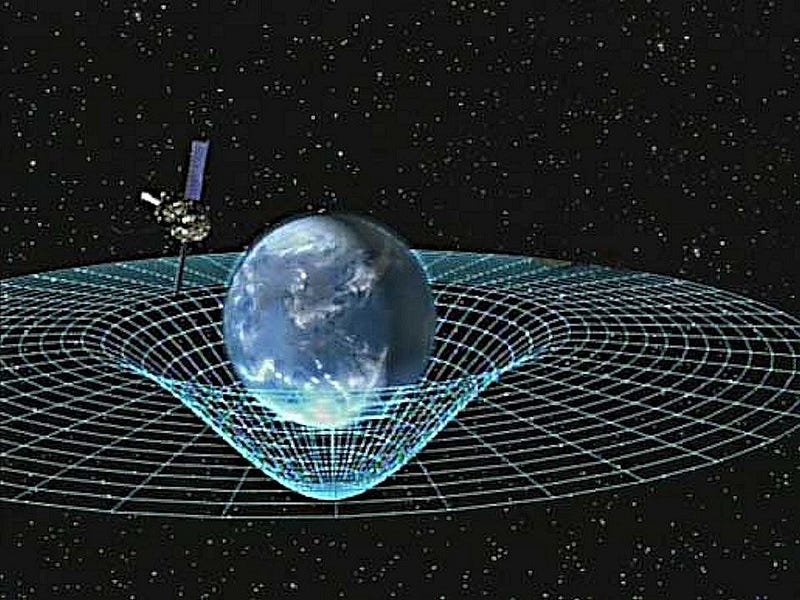
The curvature of space means that clocks that are deeper into a gravitational well — and hence, in more severely curved space — run at a different rate than ones in a shallower, less-curved portion of space. (NASA)

If the Sun were to simply wink out of existence, disappearing from the Universe, we wouldn’t know for some time. Earth wouldn’t immediately fly off in a straight line; it continue orbiting the Sun’s location for another 8 minutes and 20 seconds. It isn’t mass that determines gravitation, but rather the curvature of space, which is determined by the sum of all the matter and energy in it.

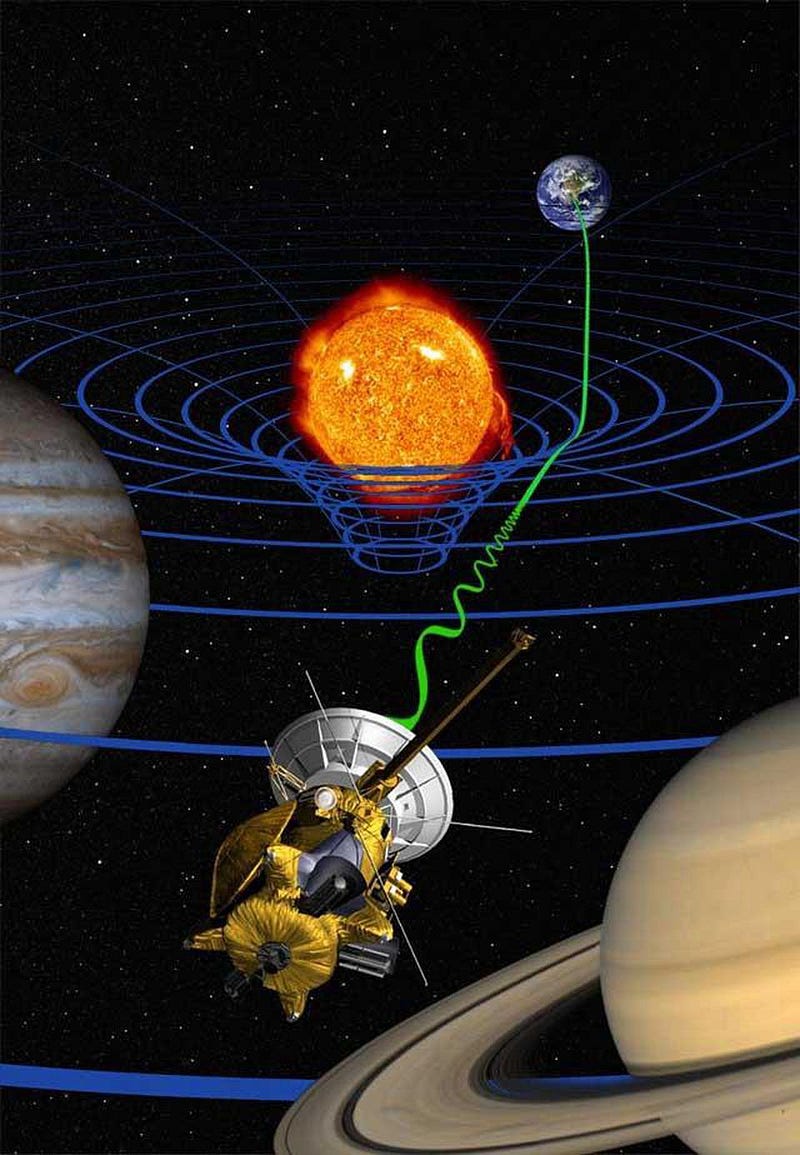
If you were to take the Sun away, space would go from being curved to being flat, but that transformation isn’t instantaneous. Because spacetime is a fabric, that transition would have to occur in some sort of “snapping” motion, which would send very large ripples — i.e., gravitational waves — through the Universe, propagating outward like ripples in a pond.

Whether through a medium or in vacuum, every ripple that propagates has a propagation speed. In no cases is the propagation speed infinite, and in theory, the speed at which gravitational ripples propagate should be the same as the maximum speed in the Universe: the speed of light. (Sergiu Bacioiu from Romania)

The speed of those ripples is determined the same way the speed of anything is determined in relativity: by their energy and their mass. Since gravitational waves are massless yet have a finite energy, they must move at the speed of light. Which means, if you think about it, that the Earth isn’t directly attracted to the Sun’s location in space, but rather to where the Sun was located a little over 8 minutes ago.

Gravitational radiation gets emitted whenever a mass orbits another one, which means that over long enough timescales, orbits will decay. Someday in the future, the Earth will spiral into whatever’s left of the Sun, assuming nothing else has ejected it previously. Earth is attracted to where the Sun was approximately 8 minutes ago, not to where it is at the moment. (American Physical Society)

This is weird, and potentially a problem, because of how well-studied the Solar System is. If the Earth were attracted to the Sun’s position ~8 minutes ago using Newton’s Laws, the orbits of the planets wouldn’t match observations. There’s another way that General Relativity is different, however. You also need to factor in the orbiting planet’s velocity as it moves around the Sun.

The Earth, for example, since it’s also moving, kind of “rides” over the ripples traveling through space, coming down in a different spot from where it was lifted up. There are two new effects going on in General Relativity that make this theory very different from Newton’s: each object’s velocity affects how it experiences gravity, and so do the changes that occur in gravitational fields.

The fabric of spacetime, illustrated, with ripples and deformations due to mass. The fabric of space curves, to be sure, but as masses move through a changing gravitational field, many interesting things happen. (Lionel Bret / Euriolos)

If you want to calculate what the spacetime curvature is at any point in space, General Relativity allows you to do it, but you need to know a few things. You need to know the locations, magnitudes, and distributions of all the masses in the Universe, just as Newton demanded. But you also need information about:

how those masses are moving and how they’ve moved over time,
how all other (non-mass) forms of energy are distributed,
how the object you’re observing/measuring from is moving in a changing gravitational field,
and how the spatial curvature is changing over time.

Only with those additional pieces of information can you compute how space is curved for you at a particular location in space and time.

It isn’t just the locations and magnitudes of masses that determine how gravity works and spacetime evolves, but rather how those masses move relative to one another and accelerate through a changing gravitational field over time. (David Champion, Max Planck Institute for Radio Astronomy)

There has to be a cost to this bending and unbending, though. You can’t just move, say, an accelerating Earth through the Sun’s changing gravitational field and not have a consequence. In fact it’s there, even though it’s small, and it can be tested. Unlike in Newton’s theory, where the Earth should trace out a closed ellipse as it orbits the Sun, General Relativity predicts that this ellipse should precess over time, and that the orbit should very slowly decay away. It might take far longer than the age of the Universe to do it, but it wouldn’t be arbitrarily stable.

Before we ever measured any gravitational waves, in fact, this was the primary method we had of measuring the speed of gravity. Not for the Earth, mind you, but for an extreme system where the orbital changes are easily observed: for a tight-orbiting system containing at least one neutron star.

The largest effects will show up for a massive object moving with a rapidly changing velocity through a strong, changing gravitational field. That’s what a binary neutron star gives us! As one or both of these neutron stars orbit, they pulse, and the pulses are visible to us here on Earth each time the pole of a neutron star passes through our line-of-sight. The predictions from Einstein’s theory of gravity are incredibly sensitive to the speed of light, so much so that even from the very first binary pulsar system discovered in the 1980s, PSR 1913+16 (or the Hulse-Taylor binary), we have constrained the speed of gravity to be equal to the speed of light with a measurement error of only 0.2%!

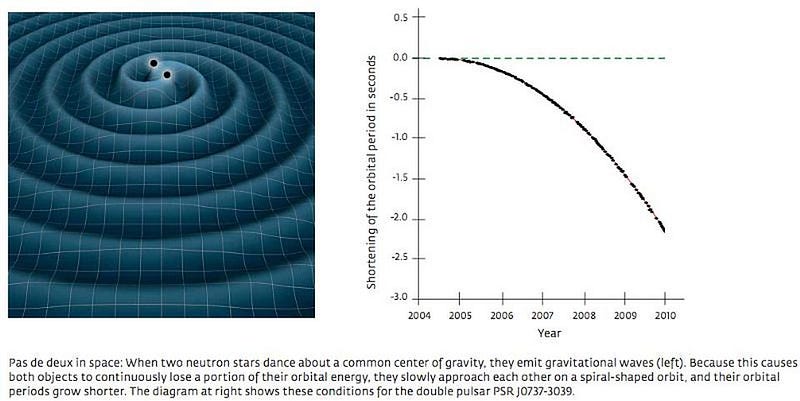
The rate of orbital decay of a binary pulsar is highly dependent on the speed of gravity and the orbital parameters of the binary system. We have used binary pulsar data to constrain the speed of gravity to be equal to the speed of light to a precision of 99.8%. (NASA (L), Max Planck Institute for Radio Astronomy / Michael Kramer (R))

Just from these binary pulsars, we learned that the speed of gravity must be between 2.993 × 10⁸ and 3.003 × 10⁸ meters per second. We can confirm General Relativity, and rule out Newton’s gravity and many other alternatives. But there isn’t a mechanism required to explain why space isn’t curved when mass was once there and now isn’t; General Relativity itself is the explanation. A mass that accelerates through a changing gravitational field will radiate energy away, and that radiated energy is a rippling through the fabric of space known as gravitational waves. Without matter or energy there any longer, there’s nothing to maintain the curvature to space. The return to its equilibrium, uncurved state, happens naturally, and simply results in gravitational radiation. It doesn’t need a further explanation. General Relativity solves it all.

Send in your Ask Ethan questions to startswithabang at gmail dot com!

Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.