Ask Ethan: Do Merging Black Holes Create An Information-Loss Paradox?
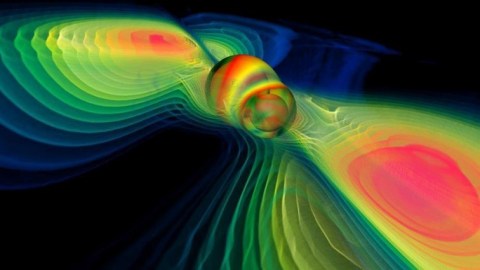
When two black holes merge together, about 5% of their mass gets lost. Where does that information go?
Do merging black holes lose information? They absolutely must, according to General Relativity and the known laws of physics. Take two black holes, merge them together, and they lose mass. For the ten black hole-black hole mergers LIGO and Virgo have seen so far, each one has lost mass in the process: about 5% of the total, on average. So where does the information that was encoded by that mass go? That’s what our Patreon supporter Pierre Fransson wants to know, asking:
When black holes merge they [lose] energy through gravitational waves. Does this pose the same problem as Hawking radiation does, with respect to loss of information? Or is the information on what has gone into the black hole somehow encoded into the gravitational wave? And if it is could we someday hope to decode what went into the black hole using gravitational waves?
Let’s take a look at black hole information in general, and then let’s examine what happens when they merge.

Black holes used to present a tremendous puzzle for astrophysicists when it came to the idea of information. No matter what it is that you make your black hole out of — whether it’s stars, atoms, protons, electrons, antimatter, heavy elements, or exotic particles — there are only three things that matter for the properties a black hole possesses: its total mass, electric charge, and angular momentum.
Whether you made a black hole out of ten solar masses of oxygen atoms, uranium atoms, or antiprotons-and-positrons should be completely irrelevant to what you find. Quantities like baryon number, lepton number, isospin, and a slew of other particle properties don’t play any role in the physics of a black hole. Once you fall inside, that information should be lost forever.
At least, that’s what happens in General Relativity all by itself.

The story changes, however, if you start to consider things like thermodynamics and quantum physics. Without those considerations, General Relativity tells you what a black hole’s entropy is: zero.
That should set off alarm bells in your head. Obviously, that cannot be right. Everything that has a temperature, energy, and particle properties has a non-zero entropy, and entropy can never decrease. If the matter that you made black holes out of had a non-zero entropy, then by throwing that material into a black hole, entropy would have to go up or stay the same; it could never go down. A black hole must have a finite, positive, and non-zero entropy to account for all the matter that falls into it.

While we conventionally think of entropy as something like “information content” or “disorder,” neither one of those definitions truly encapsulates what it physically is. Instead, it’s better to think of entropy as the number of possible configurations that a quantum state could theoretically possess.
Whenever a quantum particle falls into a black hole’s event horizon, it has a number of particle properties inherent to it, including spin, charge, mass, polarization, baryon number, lepton number, and many others. If the singularity at a black hole’s center doesn’t depend on those properties, there must be some other location that stores that information. John Wheeler was the first person to realize where it could be stored: the event horizon. By considering what an outside observer would see as a quantum particle (or a set of particles) fell into a black hole’s event horizon, we can understand how entropy — or information, if you like — gets encoded.

From far away, something falling in would appear to asymptotically approach the event horizon, spaghettifying in the process. Its apparent color would turn redder and redder due to the effects of gravitational redshift, and the amount of time to cross the horizon would asymptote to infinity, as relativistic time dilation took effect. The information from anything that falls into a black hole must appear to be encoded along the surface of the event horizon.
Since a black hole’s mass determines the size of its event horizon, this gave a natural place for the entropy of a black hole to exist: on the surface area of the event horizon. As a black hole grows, its event horizon grows, accommodating the additional entropy and information of whatever falls in.
Instead of zero, the entropy of black holes would be enormous, based on the number of quantum bits that could be encoded on an event horizon of a particular size.

And that brings us to the problem of merging black holes. We now have two of them, in orbit around one another, with a tremendous amount of entropy encoded on their surfaces. Let’s imagine we have two black holes of roughly equal masses, which more-or-less corresponds to the black hole mergers LIGO and Virgo have seen. Black hole #1 has a certain mass (M) and a amount of entropy: let’s call it S. Black hole #2, if it’s the same mass (M) as #1, also has S for its entropy.
Now, let’s imagine them merged together. In the end, the new black hole will have almost (but not quite) double the original mass; its new mass will be the sum of both black hole #1 and black hole #2, minus about 5%. All told, its total mass will be 1.9M, assuming each black hole lost 5% of its mass. This means there’s a set of gravitational waves traveling through the Universe carrying that missing energy: 0.1Mc2, where mass is converted into energy by Einstein’s famous rule.

But here’s where we run into the big conundrum that demonstrates how difficult it is to answer the question of where the entropy (or information) goes when black holes merge. You can imagine three possible solutions:
- The information from both black holes remains entirely encoded on the event horizon of the new, larger-mass black hole. The gravitational waves carry none.
- The maximal amount of information possible gets encoded onto the gravitational waves: these energy-carrying waves are also entropy-carrying waves, leaving the merger remnant with the least amount of entropy possible.
- The information gets split in some non-maximal way between the new event horizon and the gravitational waves themselves.
Unfortunately for all of us, all three possibilities are allowed.
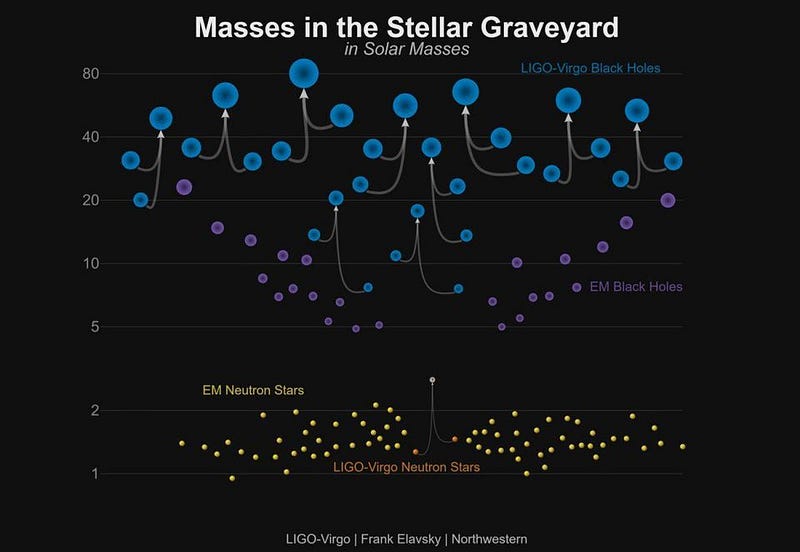
Remember what we said about the amount of entropy that a black hole can possess: it’s proportional to the event horizon’s surface area. But that surface area is proportional to the mass squared, which means that if black hole #1 had an entropy of S and black hole #2 had an entropy of S, then a black hole with 1.9 times the mass of #1 and #2 would have an entropy of ~3.6S, enough to easily hold the information of both progenitor black holes. This is the Bekenstein-Hawking entropy.
On the other hand, gravitational waves can carry entropy, too, just like any wave can. And it’s not like we can just calculate how much quantum information is in those waves like we can for photons; without an understanding of the underlying quantum (gravitational) processes at play, we are limited in how much we can say about the entropy carried by gravitational waves from merging black holes.
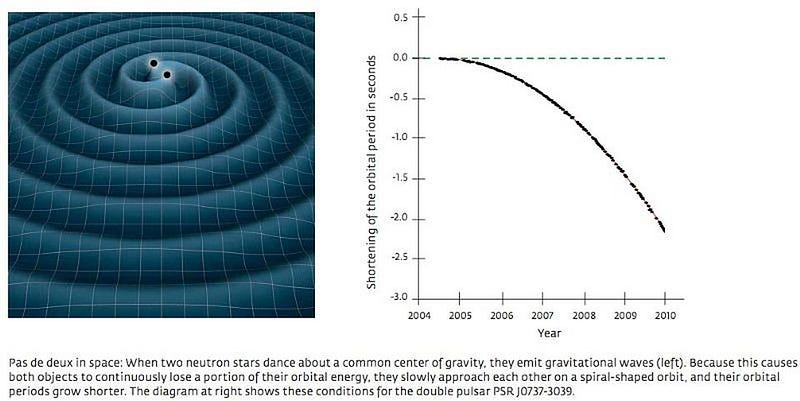
But we can say something of great importance here: the gravitational waves must carry some entropy themselves. During the inspiral phase preceding the merger, these two event horizons are practically unchanged, yet the system is losing mass and energy as the two massive black holes approach one another in space. The gravitational waves carry that energy away, and must also carry the information-and-entropy associated with that energy change with them.
Throughout the entirety of the merger, these gravitational waves are being generated by the changes in curved space itself, and the energy for those waves comes from the changing configuration of the matter-and-energy distribution of the fabric of space. But how much of the information from either of the two event horizons makes it out and into the waves, though, is a question we cannot answer at present, either theoretically or observationally.

Information doesn’t get lost when two black holes merge, since the final state is known to have a greater entropy than either initial state, so it’s not the same as the problem of Hawking radiation. But we cannot say with any certainty how the entropy encoded on those two black hole event horizons gets transferred into the new event horizon and outgoing gravitational wave system we wind up with in the end.
Observationally, we have no way of extracting any sort of entropic or informational signal from gravitational waves at present. Nor can we measure the entropy encoded on an event horizon. We have every reason to believe that information is preserved, and that most of the information from the progenitor black holes winds up in the merged product. But until we find a way to measure and quantify the entropy in black holes and gravitational waves, we must confess to our own ignorance.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.




