Ask Ethan: Do Ancient Galaxies Get Magnified By The Expanding Universe?

The farther away they get, the smaller distant galaxies look. But only up to a point, and then they get magnified. Here’s how.

Intuitively, we all know that when we see an image of an object, it could either be large and far away or small and close by. Only with a three-dimensional measurement can we actually know what’s truly the case. But the expanding Universe, because distances change over time, poses a unique challenge: more distant objects existed in a smaller Universe, admitting the possibility of a more distant object actually appearing larger than a closer, similarly sized object. Is this actually the case? That’s what Patreon supporter Ken Blackman wants to know, asking:

Do ancient galaxies appear larger to us than they really were, due to the expansion of the Universe? If so, then by how much?

The farther away you look, the smaller the same-sized object will appear. But only to a point, and then that same-sized object will actually appear larger again. Here’s the science behind this counterintuitive but very, very true phenomenon.

Even though a human head is much larger than the distance between the thumb and forefinger shown here, they appear to be the same angular size because of the relative distances from the camera. This concept of angular diameter behaves in a somewhat counterintuitive fashion in the expanding Universe. (BEATRICE MURCH / FLICKR)

Have you ever held two fingers up close to your eyes, looked at someone nearby, and pretended to squish their heads? This game, a longtime favorite among young children, only works because of the mathematics of angular size.

Unlike physical size, which is the fixed size of a solid object, the angular size of an object can be changed by moving it closer to or father away from you. A ruler that’s 12″ (30 cm) long will appear to be the same length as a 36″ (90 cm) yardstick that’s three times farther away, as a consequence of perspective. This same concept applies not only to any object viewed here on Earth, but anywhere in the Universe as well.

The angular size of anything, from rulers to galaxies, is dependent on both the actual size of the object and its distance from us.

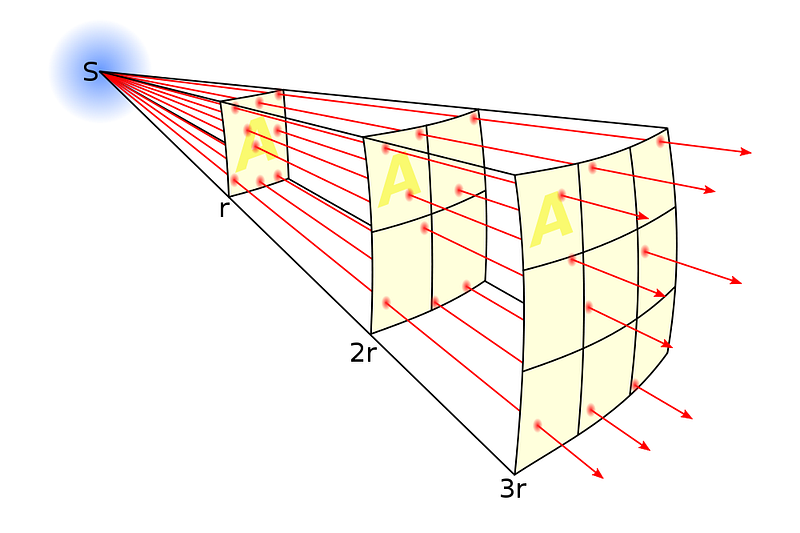
The way that sunlight spreads out as a function of distance means that the farther away from a power source you are, the energy that you intercept drops off as one over the distance squared. This also illustrates, if you view the squares from the perspective of the original source, how larger objects at greater distances will appear to take up the same angular size on the sky. (WIKIMEDIA COMMONS USER BORB)

You might think, quite naively, that the size you perceive an object to be will simply depend on its actual size and its distance from you. That if you took an object like the full Moon, which takes up 0.5° on the sky at its current distance of ~380,000 km, and moved it a thousand, million, or even a billion times farther away, it would take up a thousandth, a millionth, or a billionth of its present angular size.

This would be true if our Universe were static, spatially flat, and unevolving with time. But that description doesn’t fit our Universe at all. Quite to the contrary, the Universe itself is expanding, and doing so with an expansion rate that changes over time. If we want to understand how angular size actually works as a function of distance, our naive approximations only work on small scales: where cosmic expansion and evolution can be ignored.

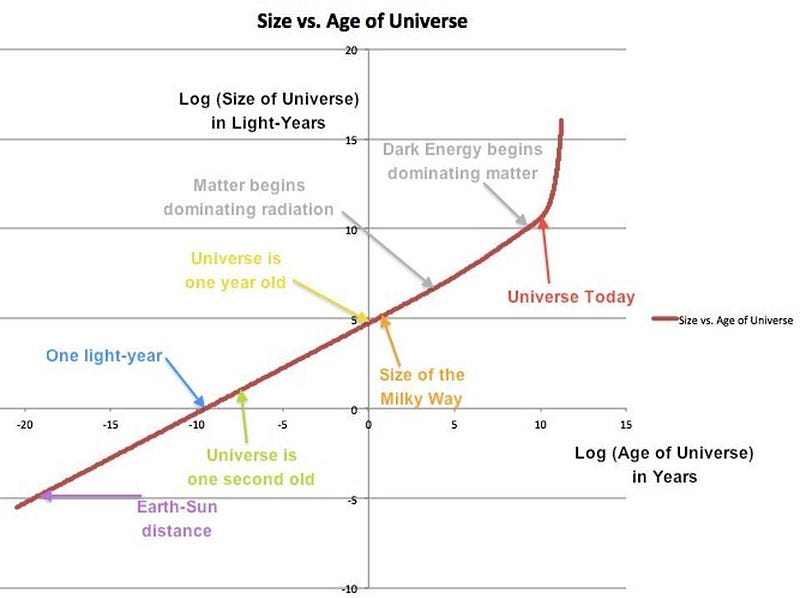
A graph of the size/scale of the observable Universe vs. the passage of cosmic time. This is displayed on a log-log scale, with a few major size/time milestones identified. Note the early radiation-dominated era, the recent matter-dominated era, and the current-and-future exponentially-expanding era. (E. SIEGEL)

But the Universe itself is expanding. Early on, radiation was the dominant factor, and the energy density dropped as both the volume increased and the wavelength of that radiation was stretched. Eventually, the radiation density dropped below the matter density (note the change in slope of the line in the graph above), and the Universe became matter-dominated, where the matter density is only affected by the growing volume of the Universe.

Finally, about 6 billion years ago, dark energy’s effects began to dominate over the effects of matter, as dark energy remains at a constant energy density regardless of the Universe’s expansion. A wide suite of evidence supports this cosmic picture, but this ever-changing expansion rate affects not only how distant various objects are from us, but also how large — in terms of angular size — they appear to be.

Two of the most successful methods for measuring great cosmic distances are based on either their apparent brightness (L) or their apparent angular size (R), both of which are directly observable. If we can understand the intrinsic physical properties of these objects, we can use them as either standard candles (L) or standard rulers (R) to determine how the Universe has expanded, and therefore what it’s made of, over its cosmic history. (NASA/JPL-CALTECH)

Imagine that the object you’re looking at is simply made of two lights: one at each end of an otherwise invisible rod. If your Universe were flat and unchanging, the angle that you saw those two lights separated by would be directly related to the distance between them and their distance from you. It would be simple geometry; nothing more.

But if your Universe is evolving in shape and size over time — which our expanding Universe consisting of radiation, matter, and dark energy most definitely is — you have to take that into account as well. You have to look at the paths that individual photons follow and remember this very important piece of the puzzle: the same sized object, billions of years ago, took up a greater proportion of the Universe’s scale than the same object does at later times.

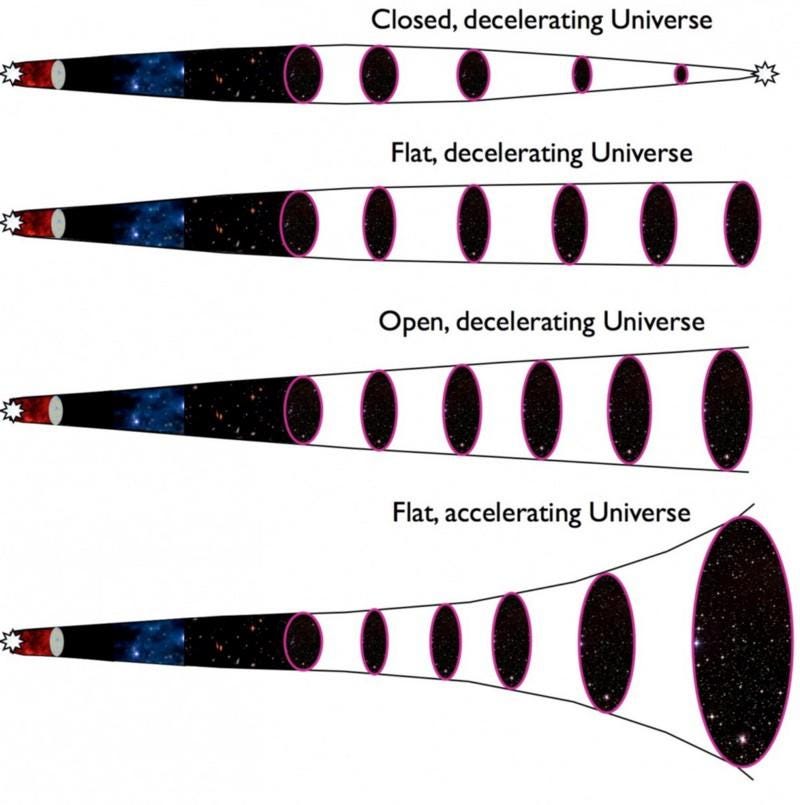
The expected fates of the Universe (top three illustrations) all correspond to a Universe where the matter and energy fights against the initial expansion rate. In our observed Universe, a cosmic acceleration is caused by some type of dark energy, which is hitherto unexplained. All of these Universes are governed by the Friedmann equations, which relate the expansion of the Universe to the various types of matter and energy present within it. Note how in a Universe with dark energy (bottom), the expansion rate makes a hard transition about 6 billion years ago. (E. SIEGEL / BEYOND THE GALAXY)

If all we had was a static Universe, the angular scale of objects would appear progressively smaller the farther away you went exactly the way you’d naively expect.

If we had an expanding Universe with nothing but matter in it, the angular scale would get progressively smaller in a quantitatively different fashion, but the farther away you looked, the same-sized object would always look smaller than a closer version of the same object.

But what we actually have is a Universe filled with dark energy, the angular scale does something very different. The farther away you look, the same-sized object looks smaller and smaller, but only to a point. Beyond that point, that object will actually start to look bigger again.

A portion of the Hubble eXtreme Deep Field in full UV-vis-IR light, the deepest image ever obtained. The different galaxies shown here are at different distances and redshifts, and allow us to understand how the Universe is both expanding today and how that expansion rate has changed over time. (NASA, ESA, H. TEPLITZ AND M. RAFELSKI (IPAC/CALTECH), A. KOEKEMOER (STSCI), R. WINDHORST (ARIZONA STATE UNIVERSITY), AND Z. LEVAY (STSCI))

You might think, when you look at a deep-field view of the Universe (such as the portion of the Hubble XDF shown above), that the smallest galaxies would also be the most distant ones. That if you had a galaxy that were the same size as our Milky Way — about 100,000 light-years across — the farther away it is, the smaller it would look.

It turns out that’s true up to a point. In our dark energy-dominated Universe, the Milky Way would take up a little more than 2 degrees on the sky if you put it at the same distance that the Andromeda galaxy is: about 2.5 million light-years. The farther away it got, the smaller it would appear, down to a minimum size of just 3.6 arc-seconds, or around 0.001 degrees.

That minimum angular size corresponds to a distance of about 14.6 billion light-years. But our observable Universe goes out farther than that: to about 46 billion light-years in all directions.

The distance/redshift relation, including the most distant objects of all, seen from their type Ia supernovae. The data strongly favors cosmic acceleration, even though other data pieces now exist. Beyond a distance of about 4.5 Gpc (which equals approximately 14.6 billion light-years), the angular size of objects will appear to increase, rather than increase. (NED WRIGHT, BASED ON THE LATEST DATA FROM BETOULE ET AL.)

We can choose to think about the Universe the same way astronomers do: to note that the sky, no matter how far back we look, always has the same number of square degrees to cover it. The physical sizes that such an angular scale corresponds to, however, will change with distance.

A typically small angular scale is one arc-second (1″), which is 1/3600th of a degree. An arc-second represents the Earth-Sun separation that we’d see if we stood one parsec (about 3.26 light-years) away. But when we talk about cosmic observables, we don’t directly measure distance, but rather redshift, which we get from seeing how significantly the spectral lines universal to all atoms and ions is shifted.

Going farther and farther away, we see that progressively more parsecs (up to a maximum of about 8,700) fit into 1″, with the maximum occurring at a redshift of ~1.5, or a distance of ~14.6 billion light-years. Beyond that distance, the same-sized object will actually take up larger angular sizes.

The farther away we look, the greater the physical distance is that corresponds to the same angular scale of 1 arc-second. Going beyond about 4.5 Gpc (14.6 billion light-years), which occurs at a redshift of z=1.5 (corresponding roughly to the onset of dark energy domination), the same-sized object corresponds to larger and larger angular scales once again. (WIKIMEDIA COMMONS USER HJB26 / PUBLIC DOMAIN)

This illustrates an incredibly bizarre phenomenon that’s incredibly useful to astronomers: if you can build an observatory that can take high-resolution images of galaxies that are 14.6 billion light-years away (at a redshift of z=1.5), then it can take even higher-resolution images of any galaxy in the Universe.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

LUVOIR, the most ambitious of the four finalists for NASA astrophysics’s flagship mission of the 2030s, proposes to put an observatory with a 15-meter diameter primary mirror in space. With that kind of power, it can achieve an angular resolution of about 10 milli-arc-seconds, corresponding to physical sizes that reach a minimum of somewhere between 300 and 400 light-years.

That means, if we construct that telescope, we’ll be able to resolve individual star clusters and star-forming regions that are that scale or larger for every single galaxy in the Universe.

A simulated image of what Hubble would see for a distant, star-forming galaxy (L), versus what a 10–15 meter class telescope like LUVOIR would see for the same galaxy (R). The astronomical power of such an observatory would be unmatched by anything else: on Earth or in space. LUVOIR, as proposed, could resolve structures as small as ~300–400 light-years in size for every single galaxy in the Universe. (NASA / GREG SNYDER / LUVOIR-HDST CONCEPT TEAM)

If you want to know how large an object actually will appear in the expanding Universe, you need to know not only its physical size, but the physics of how the Universe expands over time. In the Universe we actually have — which is composed of 68% dark energy, 27% dark matter, 5% normal matter and about 0.01% radiation — you can determine that objects will appear smaller the farther away they get, but then the physics of the expanding Universe magnifies them once again the farther away you look.

It might surprise you to learn that the most distant galaxy we’ve ever observed, GN-z11, actually appears twice as large as a similarly sized galaxy that’s only half the distance away from us. The farther away we look, beyond a specific critical distance, objects actually appear larger the farther away they get. Even without gravitational lensing, the expanding Universe alone makes ultra-distant galaxies appear larger to our eyes.

The most distant galaxy ever discovered in the known Universe, GN-z11, has its light come to us from 13.4 billion years ago: when the Universe was only 3% its current age: 407 million years old. An equivalent galaxy located half the distance away would actually appear half the size of GN-z11, owing to the counterintuitive effects of the expanding, dark energy-rich Universe. (NASA, ESA, AND G. BACON (STSCI))

Send in your Ask Ethan questions to startswithbang at gmail dot com!

Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.