Ask Ethan: Are there different types of space and time?

If everything is relative, as Einstein says, then how do cosmologists measure these quantities in ways everyone can agree?

“A human being is part of a whole, called by us the Universe, a part limited in time and space. He experiences himself, his thoughts and feelings, as something separated from the rest a kind of optical delusion of his consciousness. This delusion is a kind of prison for us, restricting us to our personal desires and to affection for a few persons nearest us. Our task must be to free ourselves from this prison by widening our circles of compassion to embrace all living creatures and the whole of nature in its beauty.” –Albert Einstein

One of the most counterintuitive lessons of Einstein’s relativity is that there’s no such thing as absolute space or absolute time. If I ask you when and where you are, you can tell me; but if you and I go to distant locations and I ask you when and where you perceive me to be, what you answer and what I answer won’t necessarily match up. As it turns out, there’s no universally good way to define time and space (or distances) for any location other than your own in general relativity. As a result, we have multiple ways of defining these things, and that’s what Patreon supporter Thomas Sola wants to know about:

I’d love to see your explanation of conformal time and comoving distance… what they are and when and how they’re used as compared to colloquial time and distance.

When we use concepts like “time” and “distance” in our everyday language, there are a host of assumptions we rarely think about.

If you think you can tell me that it’s 10:05 AM where I am and that I’m located 2,400 feet away from you, you may not realize why you think you can tell me that. You assume that your clock and my clock run at the same speed, that they originated at a common point where we agreed upon what time means, and that when we bring those two clocks back together again, they’ll be in agreement once again. Simple enough, right?

Except this only happens if two important things are true:

1. Nothing is moving relative to anything else. If any two things obtain a relative velocity with respect to one another, they experience the passage of time (and their perception of distance) differently from one another. Unstable particles moving close to the speed of light appear to live longer because of time dilation, and astronauts aboard the ISS, in rapid motion around the Earth, age at a slightly (but perceptibly) different rate from stationary humans on Earth. And…
2. Space is completely flat, which it never is. In our Universe, we’re governed by general relativity, which tells us that the existence of matter and energy mean that space is curved, and that clocks run at different rates depending on how deep of a gravitational field they’re in. A clock at the top of the Empire State building will run a few microseconds slower every year than one at the bottom.

For distances, those same constraints are true: motion and the curvature of space both make it inherently impossible for observers at different locations to necessarily agree on a universal standard of distance. But there’s something extra that comes into play if we start looking at really large distances: the fact that the fabric of the Universe itself — space — is expanding on a cosmic scale. No longer can we talk about the distance between galaxies as things that we can measure with an agreed-upon ruler, because the space between those galaxies expands over time. This gets us into trouble when we talk about, for example, measuring the most distant galaxy in the Universe.

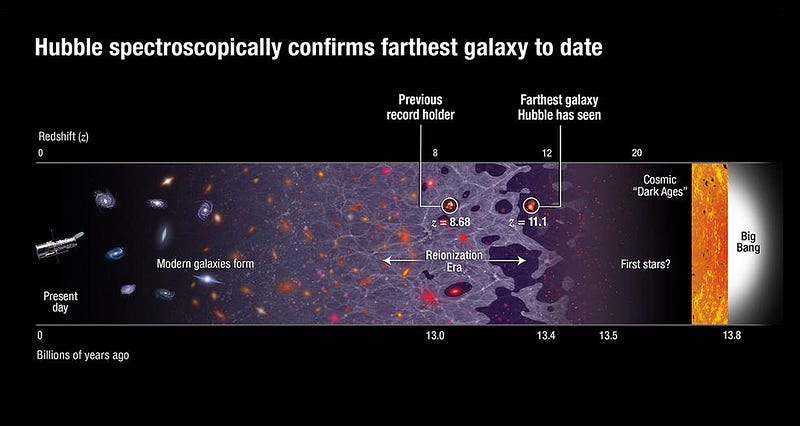
The current cosmic record-holder is located at a redshift of 11.1, which means that — in our 13.8 billion years since the Big Bang — its light is only reaching us now after journeying for 13.4 billion of those years. But how far away is that galaxy? You might think, based on light-travel-time, that it’s 13.4 billion light years away, but that’s hardly fair. At the time the light reaching us right now was emitted, that galaxy was less than two billion light years from us. Thanks to the expansion of the Universe, using our conventional standards of measurement, that galaxy is around 32 billion light years away. A universal standard of distance is hard to define in an expanding Universe, where distances change over time.

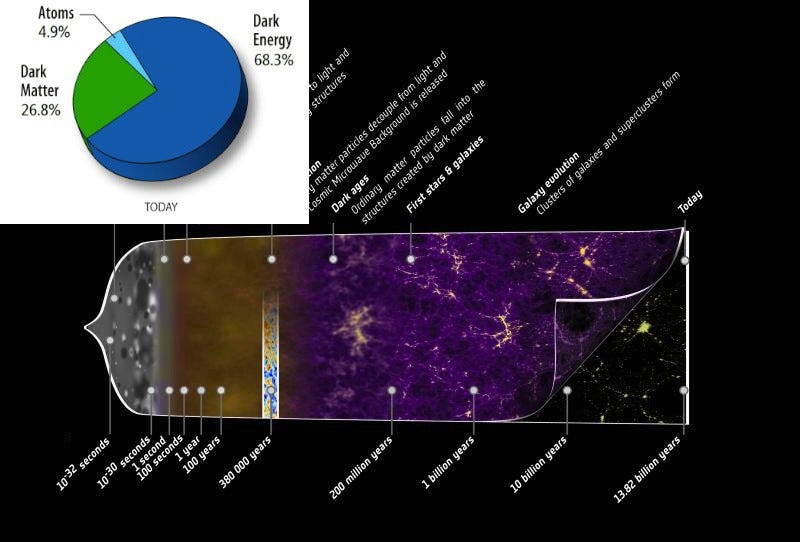
So one of the things we introduce, to address Thomas’ question, is the concept of different types of distances. The one he asks about in particular — comoving distance — is one of my favorites: it simply recognizes that distances in the Universe are changing due to the Hubble expansion, and so it scales the expansion out. This is incredibly useful when we’re doing simulations of how structures like stars, galaxies and clusters-and-filaments form in the Universe. Sure, gravitation is at work, but the Universe is expanding the whole time as well. By knowing how to scale the distances to the expansion (i.e., by using comoving distances), we can see how the large-scale structure of the Universe evolves. Visually, this gives us a much more interesting way to look at things than to watch the Universe expand and try to pick out structure formation amidst an expanding Universe.

And because space and time are inextricably linked into a unified concept — spacetime — it’s necessarily true that we need a new concept of time to correspond to each individual concept of distance we come up with. The time counterpart of comoving distance is, in fact, conformal time. If you were to magically (and it would be an act of magic) “freeze” the expansion of the Universe, everywhere, instantaneously, conformal time corresponds to how long it would take a light ray to travel from one location directly to you.

For the most distant galaxy in the Universe, that corresponds to a conformal time of 32 billion years. For the perceived location of the hot Big Bang, that corresponds to a conformal time of 46 billion years. This is true, even though only 400 million years passed between the Big Bang and the emission of light from that distant galaxy; the expansion of space was so rapid early on — and those differences propagate to today — so that a 14 billion year difference in conformal time corresponds to a “proper time” (which is what we typically assign the meaning of “time” to) difference of just 400 million years.

If you’re talking about things here on Earth and nothing’s moving close to the speed of light or changing in its gravitational field very much, all of the different types of “distance” and “time” you can use are pretty much the same. But if you’re talking about the expanding Universe on a large, cosmic scale, proper distance and proper time might not be as useful (or interesting) to think about as comoving distance and conformal time. The next time you see a simulation of the Universe, and you note that it doesn’t appear to be expanding, be aware that’s because the simulation is using comoving distance, even though it may also be using proper time.

And when you hear talk of a super-distant object that’s assigned a distance of less than 14 billion light years, keep in mind that’s likely also a use of comoving distance. According to our conventional, proper rulers, it’s likely to be much farther than that!

Submit your Ask Ethan questions to startswithabang at gmail dot com!

This post first appeared at Forbes, and is brought to you ad-free by our Patreon supporters. Comment on our forum, & buy our first book: Beyond The Galaxy!