Ask Ethan #90: Muons, relativity & a new record?
How one of the first tests of special relativity might lead to the greatest particle accelerator of all-time.
“One feels that the past stays the way you left it, whereas the present is in constant movement; it’s unstable all around you.” –Tom Stoppard
Every naturally occurring thing we’ve ever observed in the entire Universe is made out of the same few particles: protons, neutrons and electrons, along with photons. At least, that’s what you might commonly think, but mixed in with that are huge numbers of neutrinos and antineutrinos, a supermassive amount of dark matter, as well as — at any given moment — a slew of unstable, high-energy particles. One of them, the muon, was the topic of the most interesting question I saw submitted for this week’s Ask Ethan, courtesy of someone who just goes by the handle MegaN00B:
Recently in one of your blogs you mentioned that a cosmic ray would strike the atmosphere, would create particles (I think a muon), & how relativity would allow the muon to travel further that it would be able to, since it would decay before it would hit our surface, even though it should have decayed before that distance would have been [traversed].
How would the muon ‘see’ this trip?
Let’s go to the very beginning here, and tell you all about the muon to start.

Almost everything we know of — all the atoms, molecules, planets, stars, nebulae and galaxies — are made out of only a few of the known fundamental particles: photons, electrons, and the gluons and up-and-down quarks that make up the protons and neutrons. There are neutrinos and antineutrinos which interact only rarely, as well as dark matter whose presence is only known gravitationally. Everything else that can be made, all the other fundamental particles that exist, they’re all intrinsically unstable, meaning that they’ll decay into something lighter and more stable over time.
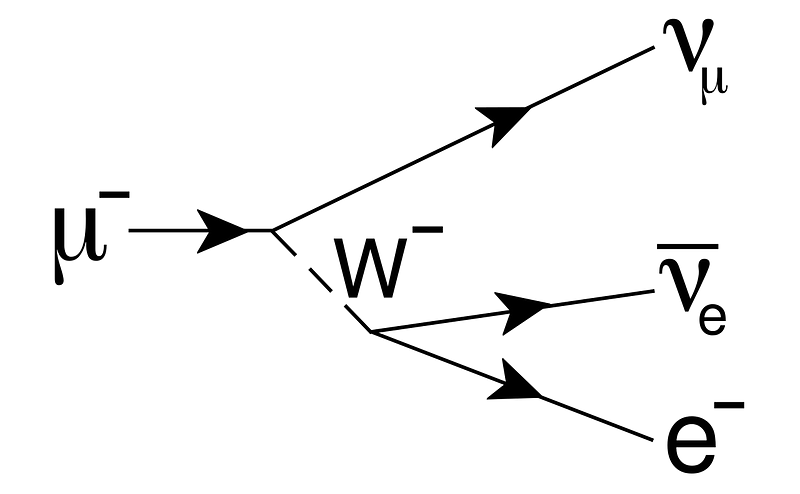
Of all the unstable particles, the muon is the closest to actually being stable, living a “whopping” 2.2 microseconds on average, orders of magnitude longer than any other particle. It’s sort of a heavy cousin of the electron, having all of the same properties:
- lepton number,
- electric charge,
- spin,
- magnetic moment,
except for the fact that it’s some 206 times heavier, and that after its quantum fate is decided, it decays into an electron (and two neutrinos).
The odd thing — or the thing that might seem odd — is that if you hold out your hand parallel to the surface of the Earth, about one muon passes through it every second. These muons, as MegaN00B alludes to, originate at the top of the atmosphere, where very high-energy particles known as cosmic rays strike all the time. These cosmic rays are mostly protons, but come in at tremendously high energies: energies high enough that when they strike the atoms in the upper atmosphere, they spontaneously produce particle showers, meaning that they create matter-antimatter pairs as well as heavy, unstable particles (like pions) that can then decay (into, for example, muons).
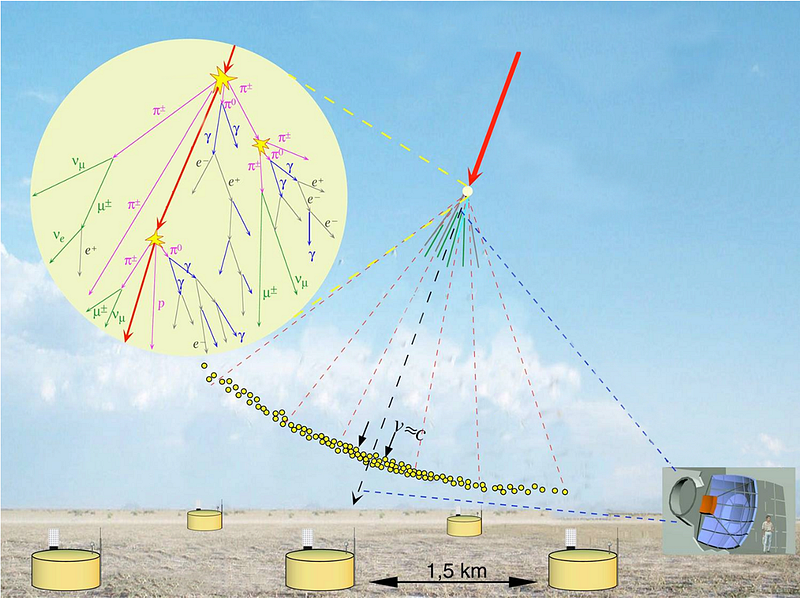
This shouldn’t surprise you: if you’ve heard of E = mc^2, then you understand that you can spontaneously create new particles of matter simply by “thwacking” two particles together at sufficiently high speeds. But let’s do the math: even if these particles are moving at almost the speed of light — 300,000 km/s — and they live for 2.2 microseconds, they should only be able to travel about 660 meters before decaying away.
Yet I told you these particles are created at the top of the atmosphere, which is some 100 kilometers, or 100,000 meters up! From our perspective, that muon should never make it to the ground. And yet, it’s Einstein to the rescue, thank to the fact that when objects move close to the speed of light, their clocks run slow.
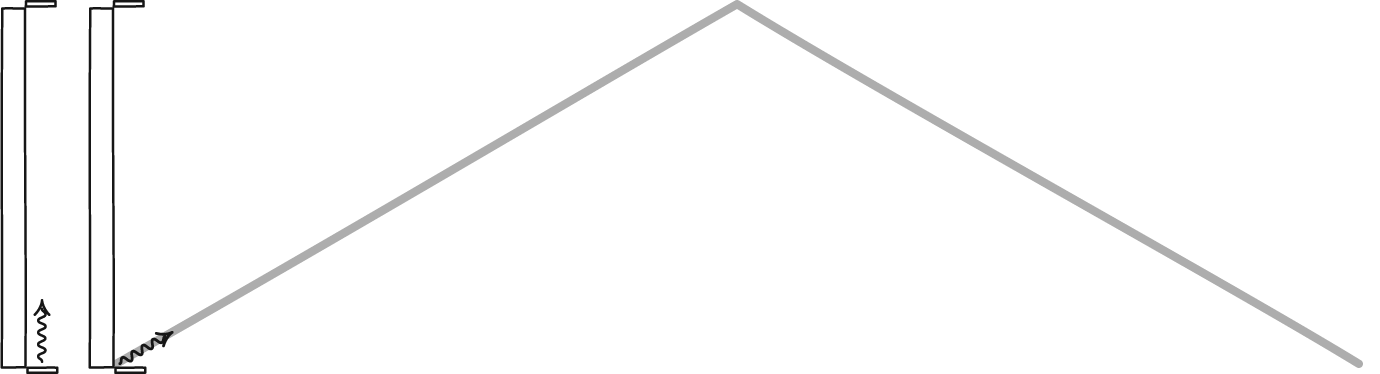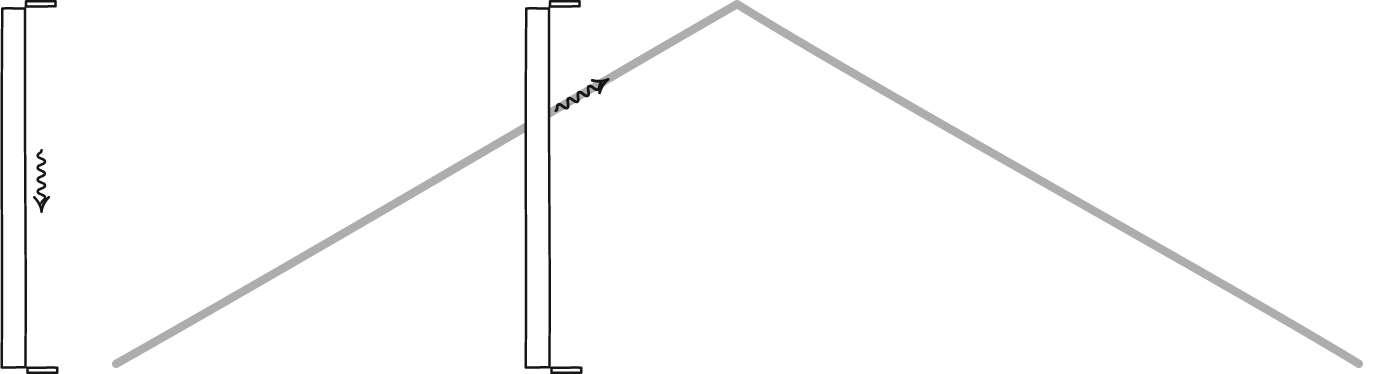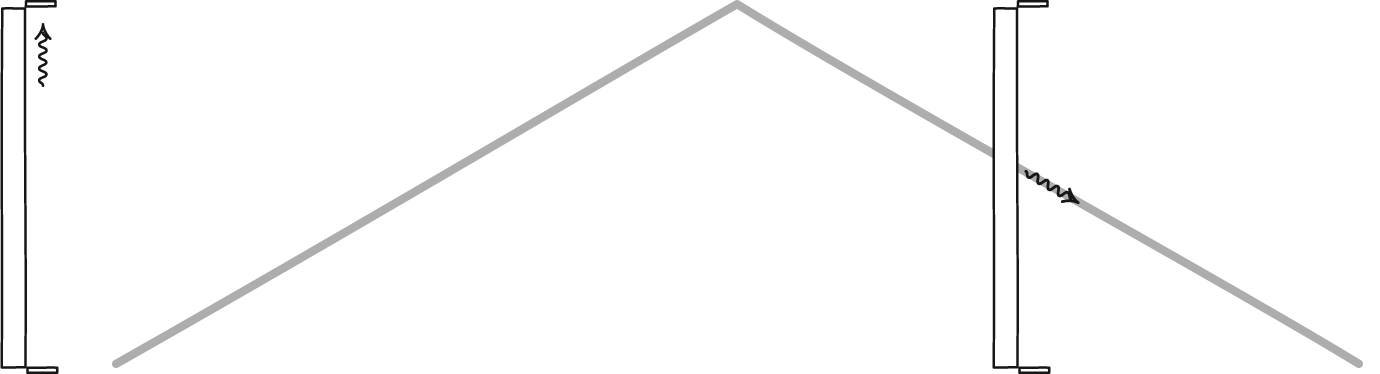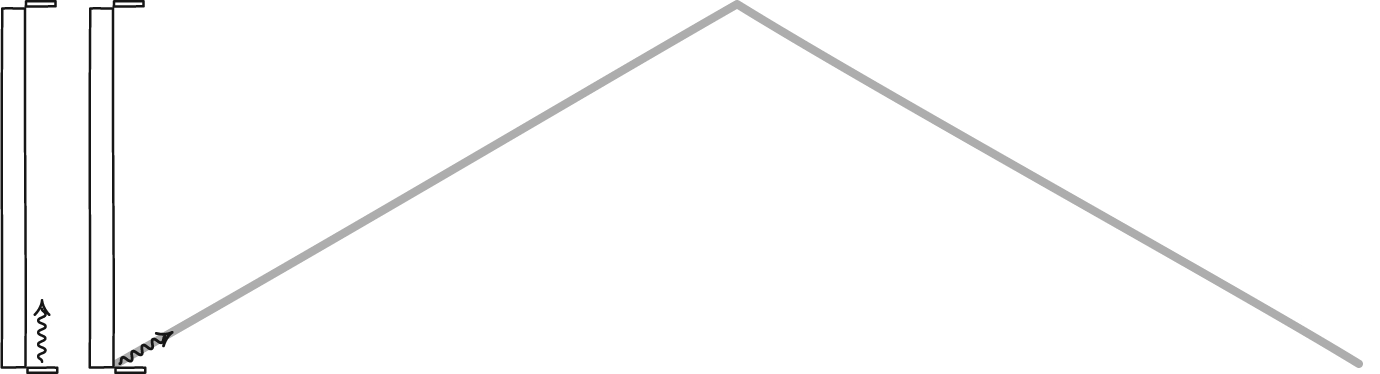
From our point of view, a muon moving at 99.9995% the speed of light will have time pass for it at just 1/1000th the rate it appears to pass at for a muon that was at rest. So instead of traveling 660 meters, on average, it can travel for 660 kilometers before typically decaying. That difference — for a muon with a mean lifetime of 2.2 microseconds — means that instead of having a one-in-10^66 chance of reaching you (which is the chance it would have if there were no time dilation), it has an 86% chance of hitting your hand.
So how would the muon perceive this? After all, in its reference frame, the muon sees time passing normally, was created at the top of its atmosphere, and has to make it all the way to the ground.
But “all the way to the ground” doesn’t mean the same thing to the muon that it does to us!
Because while the muon sees time pass normally for itself, it sees the world around moving towards it at 99.9995% the speed of light. In addition to time dilation, the muon sees the effects of length contraction, meaning that the 100 km distance it must travel appears just 1/1000th as long: a mere 100 meters. Again, it has an 86% chance of making it to the ground before decaying in this scenario, even from its point of view.
But this knowledge brings up a tantalizing possibility: if simply by accelerating them tantalizingly close to the speed of light, we can extend the muon’s lifetime, perhaps we can use this to build the ultimate particle accelerator/collider!

Normally, we’ll use a stable particle (or antiparticle), like an electron, positron, proton or antiproton in our accelerators. By applying an electric field, we can accelerate the particle, and by applying a magnetic field, we can bend it into a ring-like shape. The ring is superior to a linear accelerator, because you can use the same “track” over and over again to achieve higher and higher energies, speeding that particle up to velocities that differ from the speed of light by much less than a single kilometer-per-second.
There’s a catch, though. You see, we’d love to be able to get the same energies that the LHC (the Large Hadron Collider) gets for electron-positron colliders. When the LHC collides two protons, that collision energy is split between not only each of the three quarks in each proton, but all of the gluons deep inside. Not only are you losing almost all of your energy that you worked so hard to get in every collision, you’re also getting a tremendous bunch of “junk” out, as all the non-colliding quarks and gluons make a huge mess in your detector, too.

But you can’t physically reach the same energies for electron-positron colliders as you can for protons. In fact, before the LHC, that very same tunnel — 27 kilometers in circumference — used to be LEP, or the Large Electron-Positron collider. But while the LHC can reach energies of 13 TeV, or 13,000,000,000,000 electron-Volts, LEP was only able to reach energies of 114 GeV, or 114,000,000,000 electron-Volts. Why this factor of ~100 difference? It wasn’t because of the size of the ring (which was identical), nor even because of the strength of the magnets (which could’ve been identical and wouldn’t have made a difference), but because of the fact that when charged particles are bent and accelerated in a magnetic field, they radiate.
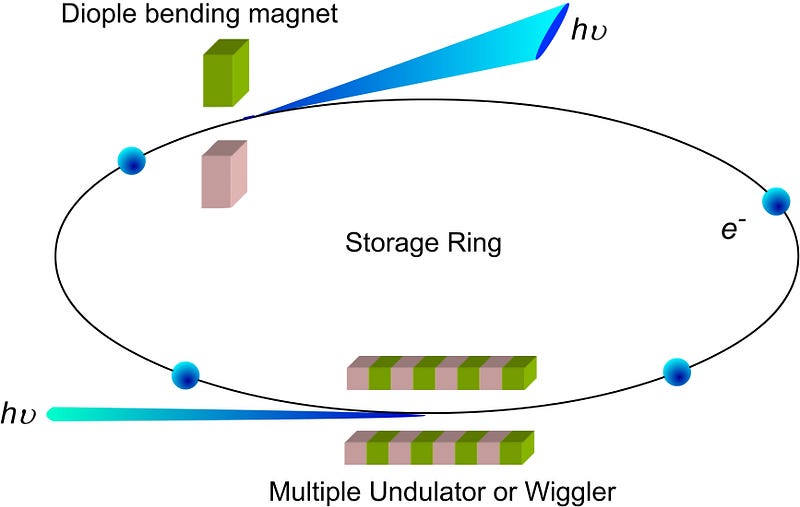
Known as synchrotron radiation, it causes accelerated charged particles to lose energy inversely proportional to their mass to the fourth power, meaning that an electron, weighing 1836 times less than a proton, loses energy at a rate that’s 10^13 times as fast! Too bad, because if you could collide electrons and positrons at the same energies you could collide hadrons, you’d be able to probe higher center-of-mass energies more cleanly, and get better data for your detector.
But if we can take advantage of the time dilation effect of muons, the ultimate machine may very well be a muon collider, as the factor of 206 in mass increase over an electron means that it would lose two billion times less energy than an electron would with every pass around the ring.

There are still challenges to overcome for building a working muon collider, but if we can collimate the muons (and antimuons) and get them into an accelerator ring with a large enough initial velocity, we should be able to accelerate them up to over 99.999% the speed of light, collide them, and discover even greater truths about the Universe — including precision physics and decays of particles like the Higgs boson, and the top quark — than ever before.
The Muon Accelerator Program spring workshop at Fermilab just wrapped up, and above is the prototype MICE 201-megahertz RF module, which boosts the muons by 11 MeV for every meter of length and while simultaneously reducing the transverse (side-to-side) velocity, necessary to keep the beam collimated. The technique used is known as ionization cooling, and hence that explains the MICE acronym: Muon Ionization Cooling Experiment (MICE).
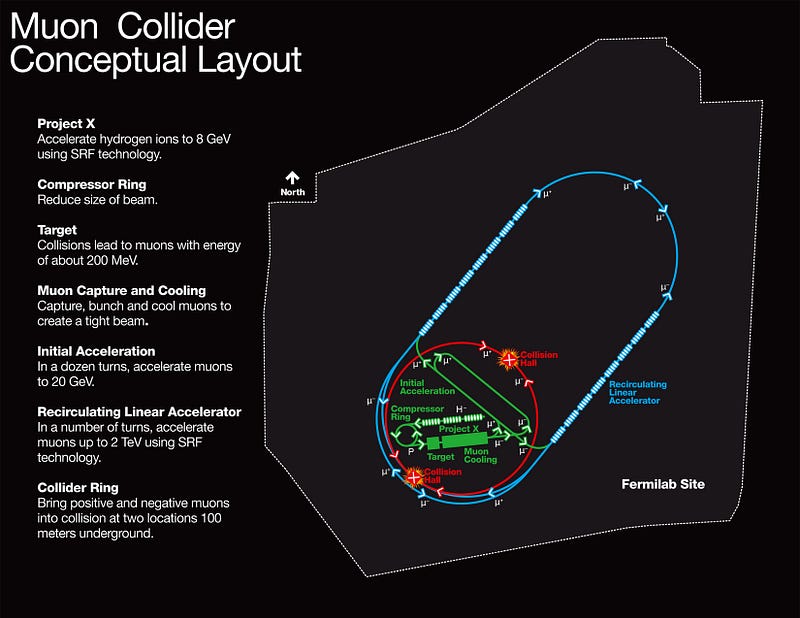
Once a pipe dream, with its detractors claiming that the muon lifetime will always be too much of a limiting factor, a circular muon accelerator/collider may very well be the very particles accelerator that opens up the next frontier of the Universe beyond what the LHC can probe. And it’s the very same physics — the physics of special relativity, time dilation and length contraction — that enables cosmic muons to reach the Earth’s surface that will make it possible! (See here for the slides of Nobel Laureate Carlo Rubbia’s talk of creating a muon-based “Higgs Factory.”)
So thanks for a good question and a great excuse to explore this fascinating frontier that may yet make the leap from science fiction into reality, MegaN00B. It’s one of the most cutting-edge Ask Ethan’s we’ve done in a long time! And if you’ve got a question or suggestion you’d like featured, submit it here. You never know, the next column could be yours!
Leave your comments at the Starts With A Bang forum on Scienceblogs.





