Ask Ethan #87: The Shape Of The Universe
With three spatial dimensions, the possibilities are tremendous. But only one answer fits what we see.
“Never erase your past. It shapes who you are today and will help you to be the person you’ll be tomorrow.” –Ziad K. Abdelnour
Even more so than we are, the Universe is shaped by the conditions it was born with. Every transition, interaction and component of it has allowed it to turn out the way we observe it to be today. But what, exactly, is that shape? After sifting through your submitted questions and suggestions, today’s Ask Ethan was chosen from reader Tom Berry, who asks:
It is my understanding that the universe is saddle-shaped. My question is, at the time of the big bang, why didn’t everything expand in all directions equally, causing a spherical shaped universe?
Let’s start by taking a dimension away, and talking about what shapes a two dimensional surface — or imaginary Universe — could have.

When you think about a two dimensional surface, you probably think of a plane: something like a flat piece of paper. You can imagine rolling it up into a cylinder, and while that might make it more of a connected surface — in that you can “exit” one side and “re-enter” on the other — but even if we do that, it’s still a flat surface.
How do you know it’s flat? One way is to draw a triangle, and add up the angles of the three angles inside. If they add up to 180 degrees, you’ve got yourself a flat surface. Also, if you draw two parallel lines, they’ll remain parallel for as far as you can draw them.
Of course, “flat” isn’t the only option for a surface’s curvature.
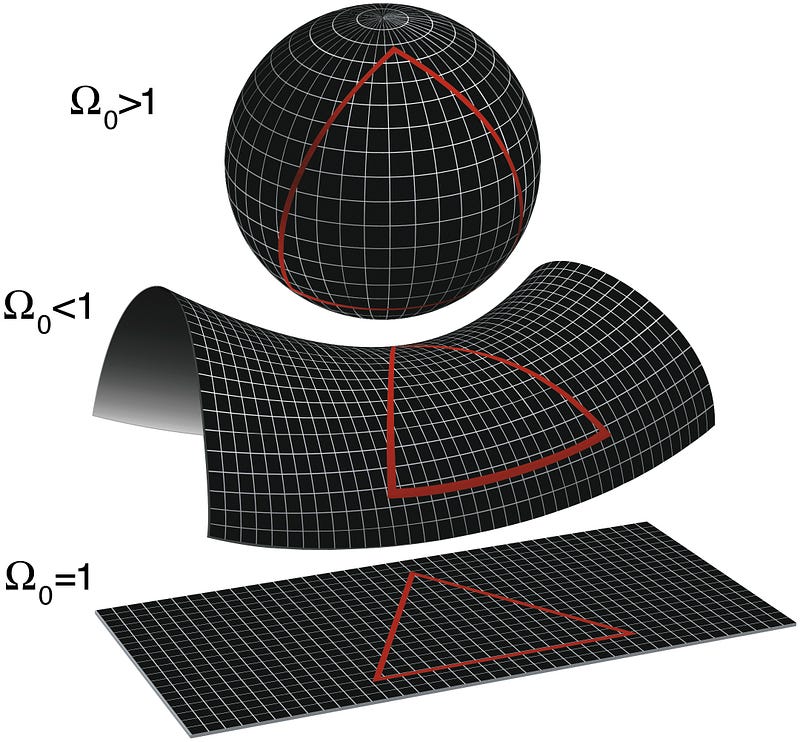
The surface of a sphere is also two dimensional, but it’s not flat. Any point you look at appears to curve “down” on both sides if you move in one direction, and also “down” on both sides if you move in the direction perpendicular to the first. If you add up the angles inside that triangle, you’ll get a number that’s greater than 180 degrees. And if you draw two parallel lines (or rather, lines that started out parallel), you’ll find — just like lines of longitude on a globe — they’ll always meet eventually, and cross in two places. (Lines of latitude, by the way, aren’t actually straight lines, with the sole exception of the equator.) This type of surface is known as a “positively curved” surface.
The surface of a saddle, on the other hand, is the other kind of non-flat two dimensional surface. It’s curved “down” in one direction (where you put your legs around the saddle) but “up” in the perpendicular direction (along the horse’s spine), which makes it a negatively curved surface. If you drew a triangle with three straight lines on a surface like this, the angles would add up to less than 180 degrees. And if you drew two initially parallel lines, you’d find that they diverged in both directions, and would wind up getting farther and farther away from one another.
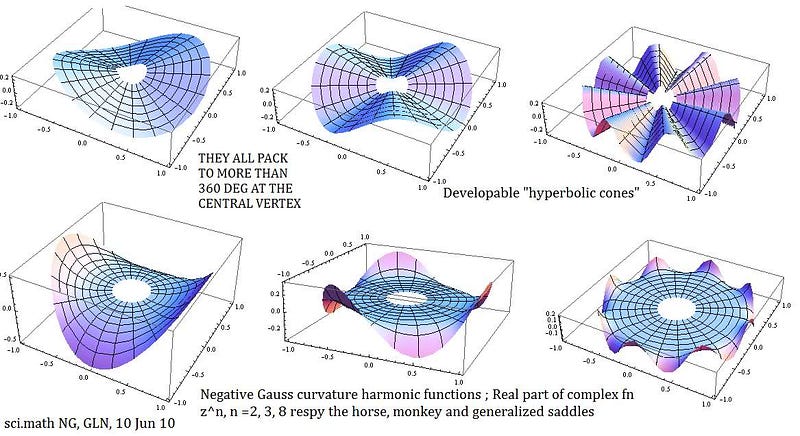
Another way to visualize this is to imagine a flat, circular piece of paper. If you cut a wedge out of this paper and re-taped the edges together, you’d create a positively-curved surface from a flat one. If you then cut a “slice” into a new circle and inserted that wedge, you’d get a negatively curved surface of some sort, like the ones shown above.
But that’s merely in two dimensions: it’s easy to visualize a surface like that from a three-dimensional viewpoint. But our three dimensional Universe is much more complicated than that.

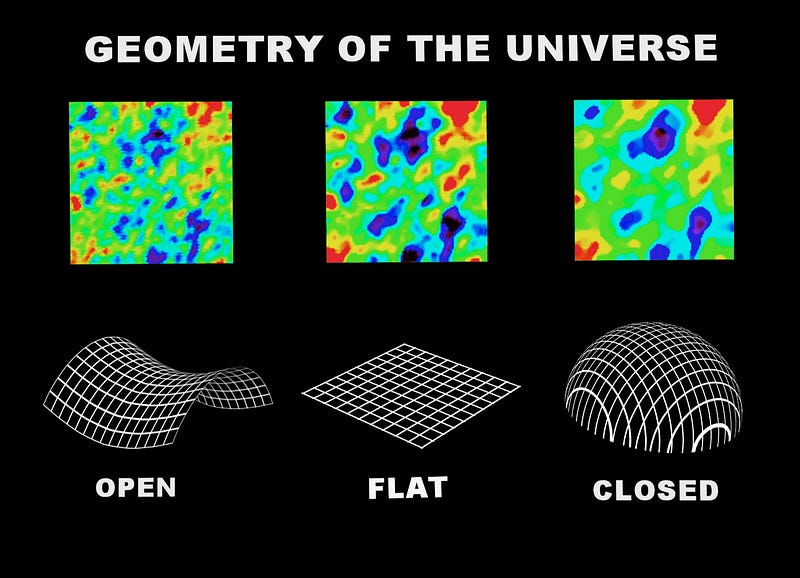
When it comes to the curvature of the Universe, there are still these three main possibilities:
- positive curvature, which is like a higher-dimensional sphere,
- negative curvature, which is like a higher-dimensional saddle,
- or zero (flat) curvature, which is like a 3-D grid.
You might think the Big Bang would prefer the “spherical” answer, since it’s pretty clear that the Universe look to be the same in all directions, but that turns out to be a red herring. There’s a compelling reason the Universe looks the same in all directions, and it doesn’t have anything to do with curvature.

The Universe looking the same at all location (homogeneous) and in all directions (isotropic) is a piece of evidence in favor of the Big Bang, which predicts that the entire Universe — everything we can observe — began from a hot, dense, uniform state where all the laws and initial conditions were the same everywhere.
As time goes on, the tiny imperfections, or departures from uniformity, give rise to structure: stars, galaxies and clusters, as well as great cosmic voids. But the reason it looks the same in all these ways and places is because everything in the Universe had a common origin, not because of curvature.
But there is a way to measure what this curvature actually is.
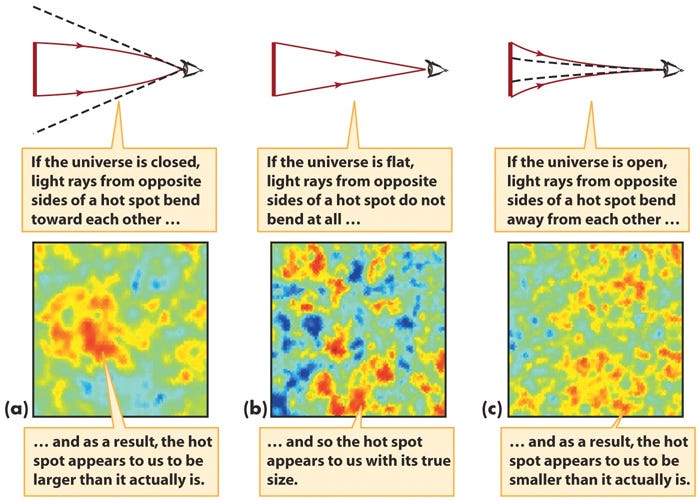
You look at the patterns of fluctuations imprinted in the cosmic microwave background! Based on how our Universe works and what it’s made out of, these fluctuations should have their “peaks” — or their hottest hot spots and coldest cold spots — on very specific angular scales. If your Universe has a negative (saddle-like) curvature to it, that scale gets biased to be a little smaller. If your Universe has a positive (sphere-like) curvature, that scale becomes biased to be larger.
The reason for this is the same reason we talked about earlier: how straight lines curve along each of these three types of surfaces. What’s true in two dimensions, even quantitatively, is still true in three dimensions in this case.
So all we need to do is observe the fluctuations in the cosmic microwave background, and we can measure the curvature of the (observable) Universe directly!
What do we find when we do exactly this?
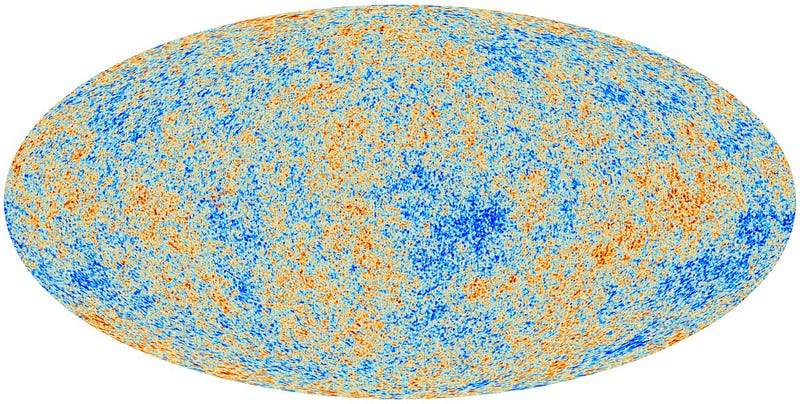
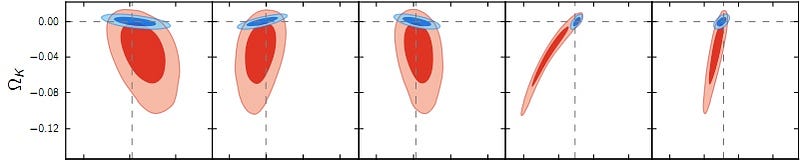
We find — quite convincingly — that the amount of curvature, shown above in the blue circles, is at most about 0.5%, which is to say that the Universe’s curvature is indistinguishable from flat.
It did expand in all directions equally, but flatness has nothing to do with that. Of course, on scales far, far larger than what we observe, the Universe could still be curved. Remember, the thing that came before, set up and gave rise to the Big Bang was a period of cosmological inflation, which takes whatever region of the Universe began inflating and stretches it, exponentially, to be ridiculously larger than its original size.
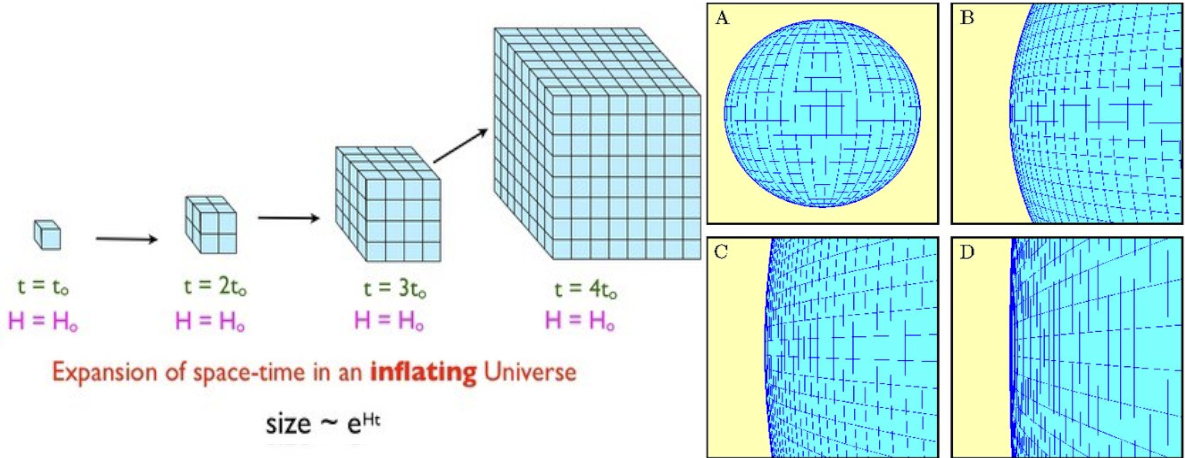
It might mean that the Universe actually is positively or negatively curved, that it’s sphere-like or saddle-like, or possibly that it’s “connected” in the sense that we can leave one end and re-enter the other. We can’t rule that out, but we can only go off of what we can observe. And from what we can see, the Universe appears to be indistinguishable from flat. But just as if you could only see what’s in the lower right panel (D) above, you’d conclude your “space” was flat, the Universe might not actually be that way. It just is, to the limits of the information available to us.
And that, Tom (and everyone), is what we know about the shape of the Universe. Thanks for a great question, and if you’ve got an idea for the next Ask Ethan column, go ahead and send it in here. I’ll see you back next week for more wonders and joys of the Universe!
Leave your comments at the Starts With A Bang forum on Scienceblogs.





