Ask Ethan #106: How, exactly, did Newton fail?
We know that Einstein’s general relativity is superior to Newton’s gravity, but where did Newton go wrong?
“To me there has never been a higher source of earthly honor or distinction than that connected with advances in science.” –Isaac Newton
Every week, you send in your questions and suggestions for what our weekly Ask Ethan column ought to feature. Sometimes, the questions are speculative about the future, sometimes, they ask about the largest scales in the Universe or the smallest particles in existence. Sometimes, they’re about space itself, or the limits of our knowledge. But for this week, I was intrigued by Francois Zinserling’s question, as he wanted to know about the longest-standing physical theory of all time… and how it fell:
Einstein’s Theory of General Relativity rules over Newton’s Laws. We get that.
What I would like to know is this; Using Newton, there is a discrepancy in the precession of Mercury’s orbit. What are we observing? Is there more gravity than we calculate by Newton, or less? Or is the problem something else?
For those of you who support my Patreon at the $3/mo. level and up, you already got a preview of the chapter that addresses this problem: the problem of Mercury’s orbit. (It’s not too late, if you want to get in!)

But this question goes a little further. As you can see, above, every planet that orbits in our Solar System goes around the Sun. In particular, it goes around not in a perfect circle, but rather in an ellipse, as Kepler noticed nearly a full century before Newton. The orbits of Venus and Earth are very close to circular, but both Mercury and Mars are noticeably more elliptical, with their closest approach to the Sun differing significantly from their greatest distance.
Mercury, in particular, reaches a distance that’s 46% greater at aphelion (its farthest point from the Sun) than at perihelion (its closest approach), as compared to just a difference of 3.4% from Earth. This part of the story has nothing to do with anyone’s theory of gravity; this is merely the conditions which these planets formed under that led to these orbital properties.
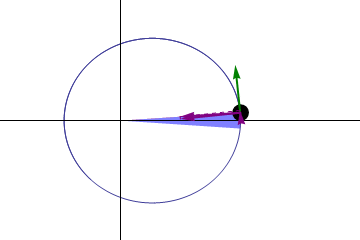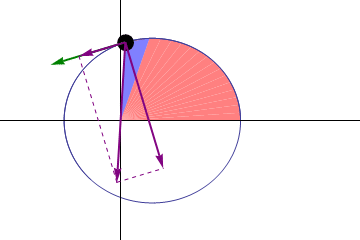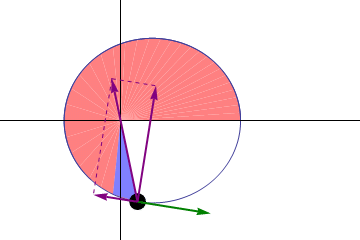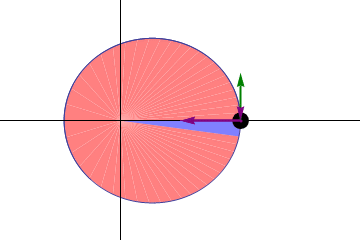
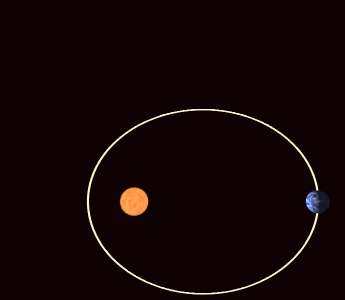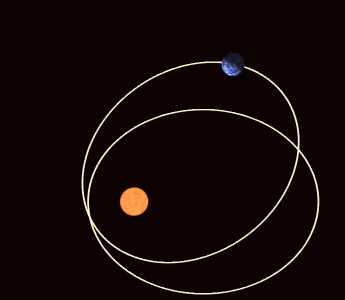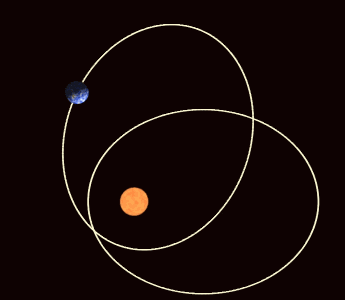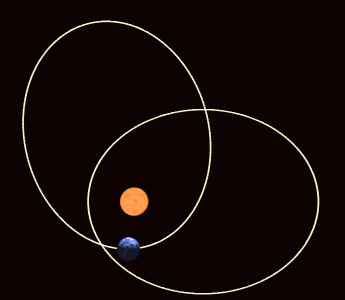
But the fact that these orbits aren’t perfectly circular means we can study something interesting about them. If Kepler’s laws were absolutely perfect, then a planet orbiting the Sun would return to the exact same spot with each and every orbit. When we reached perihelion one year, then if we counted out exactly one year, we’d expect to be at perihelion once again, and we’d expect the Earth to be in the same exact position in space — relative to all the other stars and the Sun — as it was the year before.
But we know Kepler’s laws can’t be perfect, because they only apply to a massless body in orbit around a massive one, with no other masses present at all. And that doesn’t describe our Solar System at all.
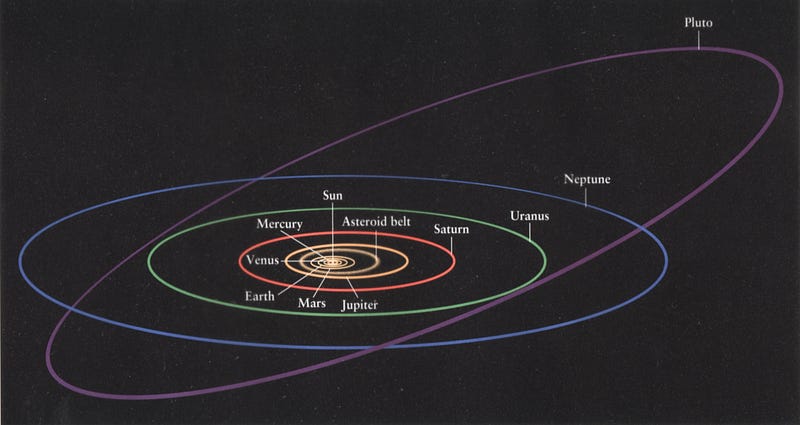
We have all these other massive bodies — planets, moons, asteroids, etc. — in addition to just a single planet orbiting our Sun. In addition, the planet we’re measuring itself has mass, meaning that it doesn’t orbit the center of the Sun, but rather the center-of-mass of the planet/Sun system. And finally, for any planet that we look at that isn’t Earth, we have this other confounding feature: our planet precesses on its axis, which means that there’s a difference between how we mark time (a tropical year, which refers to the seasons and the calendar) and how the Earth returns to the same position in space (a sidereal year, which refers to a single complete orbit) from year-to-year.
So we have to take all of these features into account if we want to predict how much another planet’s orbit would appear to change over time. With everything we know about Earth, Mercury, and all the other masses we’ve observed and measured, what do we expect?
For starters, the difference between a sidereal year and a tropical year is slight, but important: a sidereal year is 20 minutes and 24 seconds longer. This means that as we mark the seasons, the equinoxes and the solstices, they occur on a calendar year basis, but our perihelion shifts ever so slightly relative to that. If a circle is a 360°, then going from January 1st of one year to January 1st of the next “only” gets us 359.98604° of the way there, which means — if there are 60′ (arc-minutes) in one degree and 60″ (arc-seconds) in one arc-minute — that every planet’s perihelion will appear to shift by 5025″-per-century. That shift, if you’re wondering, appears as an advance in the orbit.
But then there are also the effects of planetary masses to take into account.
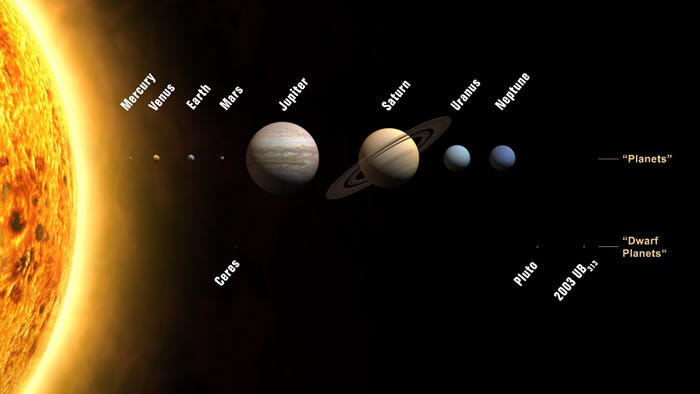
Each planet will affect the motion of another differently depending on its relative distance, its mass and its orbital proximity, as well as whether it’s interior or exterior to the planet in question. Mercury, being the innermost planet, is arguably the easiest one to do the calculation for: all of the planets are outer to it, and hence they all cause its perihelion to also advance. Here are the effects of those planets, in order of decreasing importance:
- Venus: 277.9″-per-century.
- Jupiter: 153.6″-per-century.
- Earth: 90.0″-per-century.
- Saturn: 7.3″-per-century.
- Mars: 2.5″-per-century.
- Uranus: 0.14″-per-century.
- Neptune: 0.04″-per-century.
The other effects, like the massiveness of the individual planet in question itself, the Sun’s motion around the Solar System’s barycenter, the contribution of the asteroids and the Kuiper belt objects, and the oblateness (non-sphericity) of the Sun and planets, all contribute 0.01″-per-century or less, and so can be safely ignored.
All told, these effects add up to 532″-per-century of advance, which gives us a total of 5557″-per-century when we add in the effects of the Earth’s precession. But when we look at what nature actually gives us, we saw that there’s more: we get 5600″-per-century of perihelion advance. In fact, this was known back in the late 1800s, thanks to the incredible observations of Tycho Brahe going back to the late 1500s! When you have a 300 year baseline of observations, you can detect effects that small.
There’s more precession than Newton predicts, and the big question is why. There were a few hints, if we knew where to look.
The first idea was that there was a planet interior to Mercury with the right properties to cause that additional advance, or that the Sun’s corona was very massive; either one of those could cause the additional gravitational effects needed. But the Sun’s corona isn’t massive, and there is no Vulcan (and we’ve looked!), so that’s out.
The second idea came from two scientists — Simon Newcomb and Asaph Hall — who determined that if you replaced Newton’s inverse square law, which says that gravity falls off as one over the distance to the power of 2, with a law that says gravity falls off as one over the distance to the power of 2.0000001612, you could get that extra precession. As we know today, that would mess up the observed orbits of the Moon, Venus and Earth, so that’s out.
And the third hint came from Henri Poincare, who noted that if you took Einstein’s special relativity into account — the fact that Mercury moves around the Sun at 48 km/s on average, or 0.016% the speed of light — you get part (but not all) of the missing precession.
It was putting those second and third ideas together that led to general relativity. The idea that there was a fabric — a spacetime — came from one of Einstein’s former teachers, Hermann Minkowski, and when Poincare applied that concept to the problem of Mercury’s orbit, there was an important step towards the missing solution. The idea by Newcomb and Hall, although incorrect, showed that if gravity were stronger than Newton’s predictions by the orbit of Mercury, additional precession could occur.
Einstein’s big idea, of course, was that the presence of matter/energy results in a curvature of space, and that the closer you are to a more massive object, the stronger gravity behaves. Not only that, but the greater the departure is from the predictions of Newtonian gravity as well.
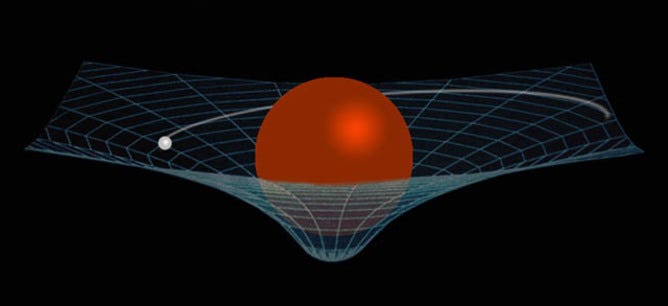
So that part answers your question, Francois, but there’s more to the story. When Einstein finally made enough headway on his theory to predict this additional precession, his prediction — of an extra 43″-per-century — was actually thought to be too much; the Newtonian contributions were estimated slightly incorrectly, and so only 38″-per-century were predicted at the time. This discrepancy was cited as an argument against general relativity, or that general relativity at best would be an approximation to the correct step forward.
It really took the prediction that light would be bent when passing by a massive body — like the limb of the Sun — to test whether Newton’s or Einstein’s theory was correct.

Newton’s theory predicted, if we want to be literal about it, that starlight would not deflect at all when it passed by the Sun, since light is massless. But if you assigned light a mass based on Einstein’s E = mc^2 (or m = E/c^2), you could find that starlight should deflect by 0.87″ when it passed by the Sun’s extreme outer limit. For a contrast, though, Einstein’s theory gave twice that amount: 1.75″ of deflection.
These were small numbers, but a joint expedition by Arthur Eddington and Andrew Crommelin during the 1919 solar eclipse, were able to measure to the necessary accuracy. The deflection they came up with was 1.61″ ± 0.30″, which agreed (within the errors) with Einstein’s predictions, and not with Newton’s. Newtonian gravity was busted.

And that’s the story of not only Newton’s gravity being superseded, but in what way(s) Newton’s theory came up short. There have been many other victories for general relativity since (and, honestly, no failures as of yet), but in all the cases where Newton’s and Einstein’s theories differ, it’s Einstein — with stronger gravitational effects close to massive bodies — who emerges victorious. Science marches forward, but sometimes each new step takes a very long time!
Have a question or suggestion for Ask Ethan? Submit it here for our consideration.
Leave your comments at our forum, and if you really loved this post and want to see more, support Starts With A Bang and check us out on Patreon!