Are Cosmologists Fooling Themselves About The Big Bang, Dark Matter And More?

Is inertia of prior ideas the only thing keeping us from the next major revolution in science?
This post was written by Brian Koberlein. Brian is an astrophysicist and Senior Lecturer of Physics and Astronomy at the Rochester Institute of Technology. His passion is communicating science to the general public, which he mostly does on his blog, One Universe at a Time.
“Any fool can criticize, condemn and complain — and most fools do.”
–Benjamin Franklin
Richard Feynman once said of the scientific process, “The first principle is that you must not fool yourself — and you are the easiest person to fool.” The idea that scientists might be fooling themselves (whether out of ignorance or in order to preserve their jobs) is a common accusation made by skeptics of scientific disciplines ranging from climate change to cosmology. It’s easy to dismiss such criticism as unfounded, but it does raise an interesting question: how can we tell that we’re not fooling ourselves?
The popular view of science is that experiments should be repeatable and falsifiable. If you have a scientific model, that model should make clear predictions, and those predictions must be testable in a way that can either validate or disprove your model. It is sometimes assumed by critics that this means the only true sciences are those that can be done in a laboratory setting, but that’s only part of the story. Observational sciences such as cosmology are also subject to this test, since new observational evidence can potentially disprove our current theories. If, for example, I observe a thousand white swans I might presume that all swans are white. But the observation of a single black swan can overturn my ideas. A scientific theory is therefore never absolute, but always tentative, depending on whatever subsequent evidence arises.

Even though it’s technically correct, calling well established scientific theories “tentative” is a bit misleading. For example, Newton’s theory of universal gravity stood for centuries before being supplanted by Einstein’s theory of general relativity. While we can now say that Newtonian gravity is probably wrong, it is as valid as it ever was. We now know that Newton is an approximate model describing the gravitational interaction of masses, and it is such a good approximation that we still use it today for things like the calculation of orbital trajectories. It’s only when we extend our observations beyond the (very large) range of situations where Newton is valid that Einstein’s theory becomes necessary.
As we build a confluence of evidence to support a scientific theory, we can be confident that it’s valid with the small caveat of being open to new evidence. In other words, the theory can be considered “true” over the range for which it’s been robustly tested, but new regimes might uncover unexpected behavior that leads to an advancement, and a more complete picture. Our scientific theories are intrinsically tentative, but not so tentative that we can’t rely upon their accuracy. It seems a reasonable position, but it raises a challenge for well established theories. Since we can never know for sure that our experimental results are the “real” results, how can we be sure we aren’t simply reinforcing the answer we expect?
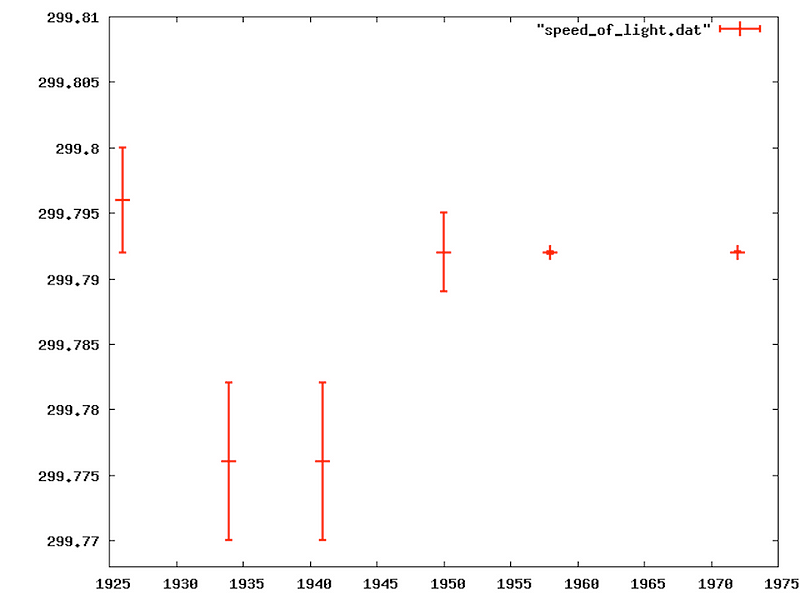
This line of thinking comes up a lot in introductory physics courses. Students are assigned to measure some experimental value such as the acceleration of gravity or the wavelength of a laser. Being novice experimenters, they sometimes make basic mistakes and get a result that doesn’t agree with the “accepted” value. When that happens, they’ll go back and check their work to find a mistake. However if they make mistakes in such a way that their errors either cancel out or aren’t apparent, they won’t tend to double check their work. Since their result is close to the expected value, they assume they must have done things correctly. This confirmation bias is something we all have, and can happen with the most experienced researchers. Historically this has been seen with things like the charge of an electron or the speed of light, where the initial experimental results were a bit off, and subsequent values tended to agree with earlier results more than the current values.
Currently, in cosmology, we have a model that agrees very strongly with observational results. It’s known as the ΛCDM model, so-named because it includes dark energy, represented by the Greek letter Lambda (Λ), and cold dark matter (CDM). Much of the refinement of this model involves making better measurements of certain parameters in this model, such as the age of the universe, the Hubble parameter, and the dark matter density. If the ΛCDM model is indeed an accurate description of the Universe, then an unbiased measurement of these parameters should follow a statistical pattern. By studying the historical values of these parameters, we can determine whether there is bias in the measurements.
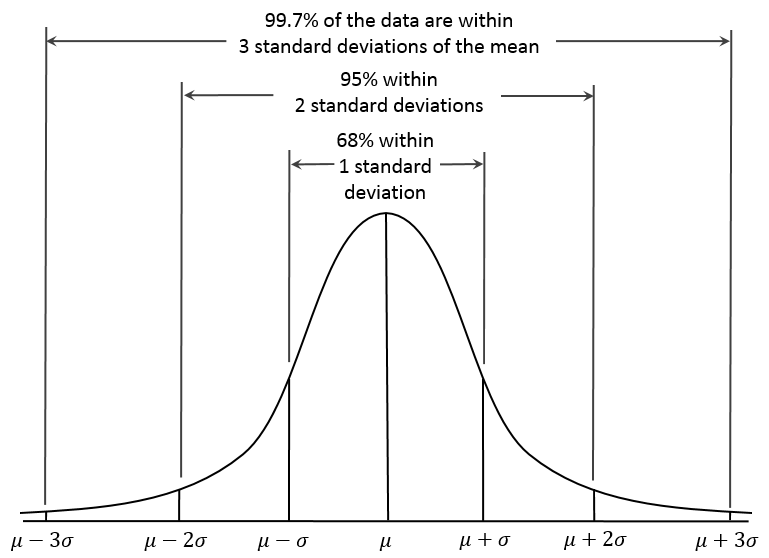
To see how this works, imagine a dozen students measuring the length of a chalkboard. Statistically, some students should get a larger or smaller value than the real value. Following a normal distribution, if the real value is 183 centimeters with a standard deviation of a centimeter, then one would expect about 8 of the students to get a result between 182–184 centimeters. But suppose all of the students were within this range. Then you might suspect some bias in the results. For example, the students might figure the chalkboard is likely 6 feet wide (182.88 centimeters), so they make their measurement expecting to get 183 centimeters. Paradoxically, if their experimental results are too good, that would lead you to suspect an underlying bias in the experiment.
In cosmology, the various parameters are well known. So when a team of researchers undertake a new experiment, they already know what the accepted result is. So are results being biased by prior results? A recent work in the Quarterly Physics Review looks at this very question. Looking at 637 measurements of 12 different cosmological parameters, they examined how the results were statistically distributed. Since the “real” values of these parameters is not known, the authors treated the WMAP 7 results as the “true” values. What they found was that the distribution of results was a bit more accurate than they should be. It wasn’t a huge effect, so it could be due to an expectation bias, but it was also significantly different from the expected effect, which could mean there was an overestimation of the experimental uncertainties. It also meant, when the 2013 Planck data came in, the “shift” in the parameters was somewhat outside the range that most cosmologists had measured.
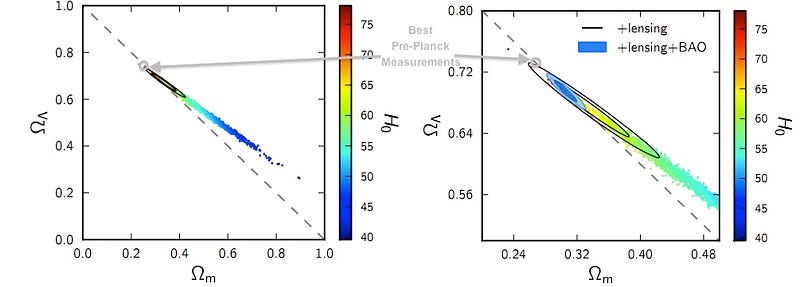
This doesn’t mean our current cosmological model is wrong, but it does mean we should be a bit cautious about our confidence in the level of accuracy of our cosmological parameters. Fortunately, there are ways we can determine whether this anomaly is due to some amount of bias, such as doing blind analysis or encouraging more open data, where other teams can do a re-analysis using their own methods and the same raw data. What this new work shows is that while cosmologists aren’t fooling themselves, there is still room for refinement and improvement of the data, methods and analyses they undertake.
Paper: Croft, Rupert A.C. et al. On the measurement of cosmological parameters. Quarterly Physics Review (2015) No 1 pp 1–14 arXiv:1112.3108 [astro-ph.CO].
Leave your comments on our forum, and check out our first book: Beyond The Galaxy, available now, as well as our reward-rich Patreon campaign!





