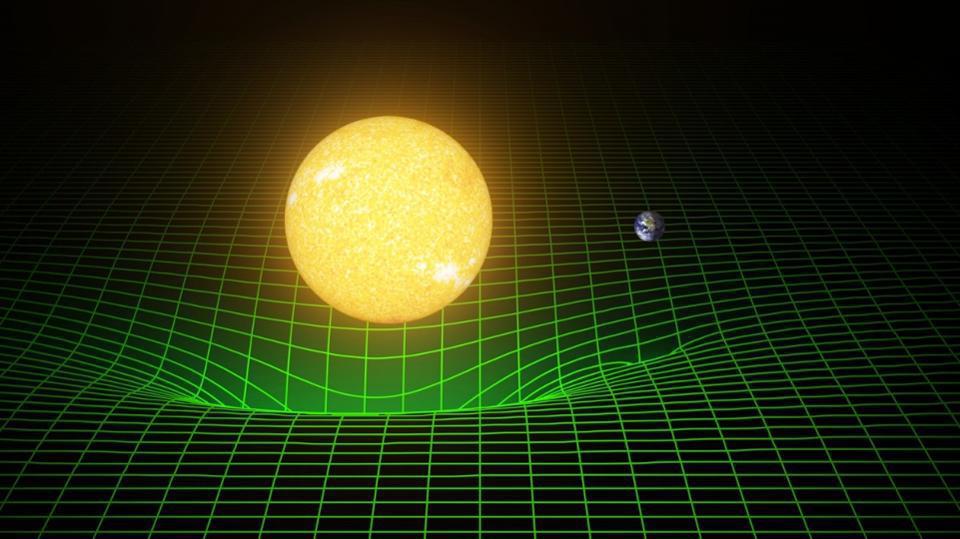
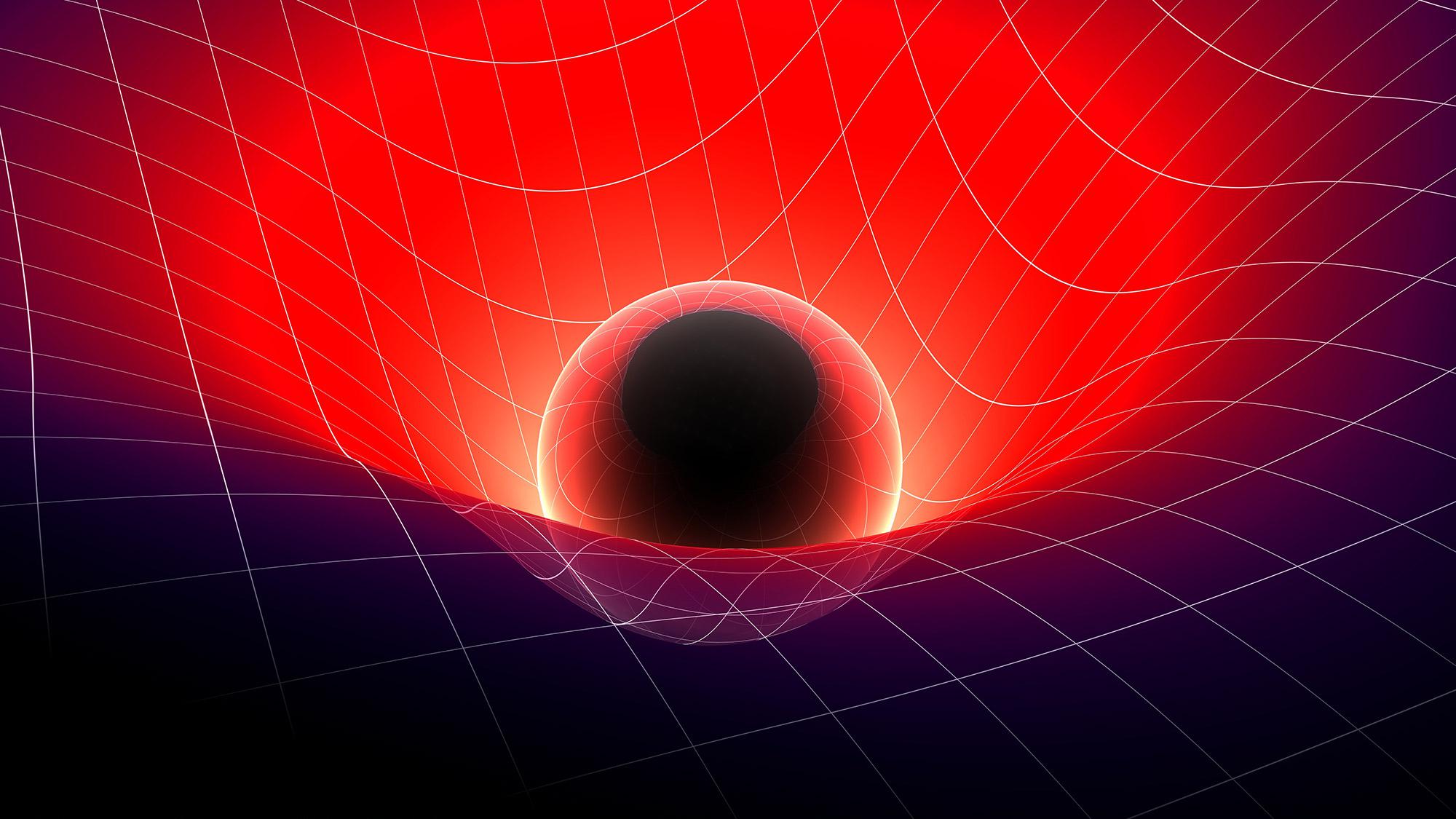
Existential physics: What is happening “now” is relative

- We always see things as they looked a little bit earlier, but we don’t normally notice this in everyday life. It gets even weirder, though.
- In special relativity, the statement that two events happened at the same time is meaningless.
- Every event is “now” for someone.
Excerpted with permission from Existential Physics: A Scientist’s Guide to Life’s Biggest Questions, written by Sabine Hossenfelder and published by Viking.
The fact that the passage of time isn’t universal is pretty mind-bending already, but there’s more. Because the speed of light is very fast but finite, it takes time for light to reach us, so, strictly speaking, we always see things as they looked a little bit earlier. Again, though, we don’t normally notice this in everyday life. Light travels so fast that it doesn’t matter on the short distances we see on Earth. For example, if you look up and watch the clouds, you actually see the clouds the way they looked a millionth of a second ago. That doesn’t really make a big difference, does it? We see the Sun as it looked eight minutes ago, but because the Sun doesn’t normally change all that much in a few minutes, light’s travel time doesn’t make a big difference. If you look at the North Star, you see it as it looked 434 years ago. But, yeah, you may say, so what?
It is tempting to attribute this time lag between the moment something happens and our observation of it as a limitation of perception, but it has far-reaching consequences. Once again, the issue is that the passage of time is not universal. If you ask what happened “at the same time” elsewhere — for example, just exactly what you were doing when the Sun emitted the light you see now — there is no meaningful answer to the question.
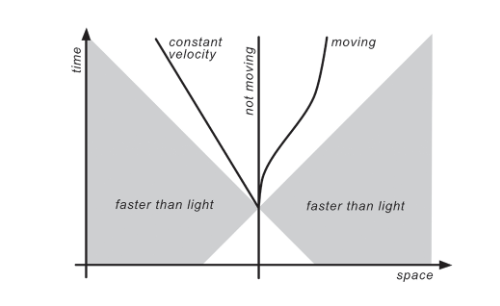
This problem is known as the relativity of simultaneity, and it was well illustrated by Einstein himself. To see how this comes about, it helps to make a few drawings of spacetime. It’s hard to draw four dimensions, so I hope you will excuse me if I use only one dimension of space and one dimension of time. An object that doesn’t move relative to the chosen coordinate system is described by a vertical straight line in this diagram (figure 1). These coordinates are also referred to as the rest frame of the object. An object moving at constant velocity makes a straight line tilted at an angle. By convention, physicists use a 45-degree angle for the speed of light. The speed of light is the same for all observers, and because it can’t be exceeded, physical objects have to move on lines tilted less than 45 degrees.
Einstein now argued as follows. Let’s say you want to construct a notion of simultaneity by using pulses of laser beams that bounce off mirrors that are at rest relative to you. You send one pulse to the right and one to the left and shift your position between the mirrors until the pulses return to you at the same moment (see figure 2a). Then you know you are exactly in the middle and the laser beams hit both mirrors at the same moment.
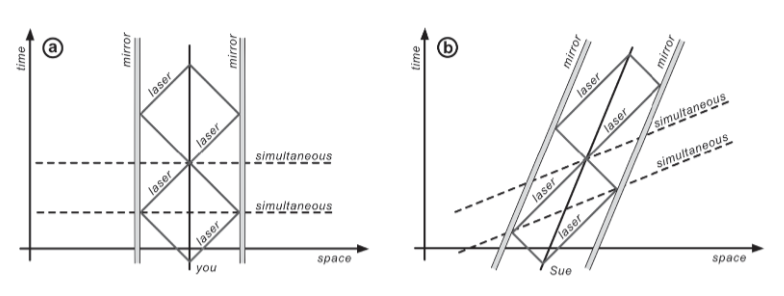
Once you have done that, you know at exactly which moment in your own time the laser pulse will hit both mirrors, even though you can’t see it because the light from those events hasn’t yet reached you. You could look at your clock and say, “Now!” This way, you have constructed a notion of simultaneity that, in principle, could span the whole universe. In practice you may not have the patience to wait ten billion years for the laser pulse to return, but that’s theoretical physics for you.
Now imagine that your friend Sue moves relative to you and tries to do the same thing (figure 2b). Let’s say she moves from left to right. Sue, too, uses two mirrors, one to her right and one to her left, and the mirrors move along with her at the same velocity — hence, the mirrors are in rest relative to Sue, like your mirrors are relative to you. Like you, she sends laser pulses in both directions and positions herself so the pulses come back to her from both sides at the same moment. Like you, she then knows that the pulses hit the two mirrors at the same moment, and she can calculate just which moment that corresponds to on her own clock.
The trouble is, she gets a different result than you do. Two events that Sue thinks happen at the same time would not happen at the same time according to you. That’s because from your perspective the pulses are moving toward one of the mirrors and away from the other. To you it seems that the time it takes the pulse to reach the mirror on her left is shorter than the time it takes for the other pulse to catch up with the mirror on her right. It’s just that Sue doesn’t notice, because on the pulses’ return paths from the mirrors, the opposite happens. The pulse from the mirror to Sue’s left takes longer to catch up with her, while the pulse from the mirror on her right arrives faster.
You would claim that Sue is making a mistake, but according to Sue, you are making the mistake because, to her, you are the one who is moving. She would say that actually your laser pulses do not hit your mirrors at the same time (figures 2c and 2d).
Who is right? Neither of you. This example shows that in special relativity the statement that two events happened at the same time is meaningless.
It’s worth stressing that this argument works only because light doesn’t need a medium to travel in, and the speed of light (in vacuum) is the same for all observers. This argument does not work with sound waves, for example (or any other signal that isn’t light in vacuum), because then the speed of the signal really will not be the same for all observers; it will instead depend on the medium it’s traveling in. In that case, one of you would be objectively right and the other one wrong. That your notion of now might not be the same as mine is an insight we owe to Albert Einstein.
We just established that two observers who move relative to each other don’t agree on what it means for two events to happen at the same time. That isn’t only odd, but it entirely erodes our intuitive notion of reality.
To see this, suppose you have two events that are not in causal contact with each other, which means you cannot send a signal from one to the other, not even at the speed of light. Diagrammatically, “not in causal contact” just means if you draw a straight line through the two events, the angle between the line and the horizontal is less than 45 degrees. But look at figure 2b again. For two events that are not in causal contact, you can always imagine an observer for whom everything on this straight line is simultaneous. You just need to choose the observer’s velocity so the return points of the laser pulses are on the line. But if any two points that are not causally connected happen at the same time for someone, then every event is “now” for someone.
To illustrate the latter step, let us say the one event is your birth and the other event is a supernova explosion (see figure 3). The explosion is causally disconnected from your birth, which means the light from it hadn’t reached Earth at the time you were born. You can then imagine that your friend Sue, the space traveler, sees these events at the same time, so they happened simultaneously according to her.
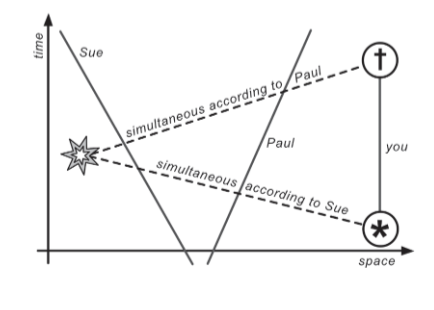
Suppose further that by the time you die the light from the supernova still hasn’t reached Earth. Then your friend Paul could find a way to travel in the middle between you and the supernova so he would see your death and the supernova at the same time. They both happened simultaneously according to Paul.