Is the world really what it appears?

Is the world really what it appears? Is what we see really what we get? Or, do our eyes have ways of playing tricks on us? Like the couple in this thumbnail. Are they old? Are they young? Are they a couple at all, or a backdrop for something else entirely?

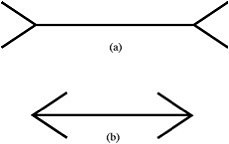
Take a look at these two lines, and decide which is longer:

Now, look at these circles. Which are lighter, and which are darker?

Actually, the lines are the same length and the circles are all the same color. These are two well-known optical illusions, that demonstrate how easy it is for our eyes to play tricks on us. And no matter how well you know the effects, they still get you. In fact, studies have shown that Line A in the first example needs to be almost twice as long as Line B (at least in Western samples) for participants to see them as equal. And I’ve certainly never been able to make the squares look the same.

But apart from being cool optical illusions, I think these examples offer profound insight into how our brains make decisions. We don’t make a decision in a vacuum. We compare to the other available options, to other possibilities, to other potential paths. And what we compare to makes a huge difference in our end choice.

Framing effects: What we see influences how we choose

In the decision literature, this concept is known as a framing effect: The frame in which a choice is presented will impact the resulting decision. Probably the best-known version of this is Kahneman and Tversky’s Asian Disease problem, a classic demonstration of Prospect Theory. Here’s the idea:

Imagine that your country is preparing for the outbreak of a disease that is expected to kill 600 people. The scientific community has come up with two programs to combat the threat. Program A guarantees that 200 people will be saved. Program B, on the other hand, has a 1/3 probability that all 600 people will be saved, but a 2/3 probability that no one will be saved. Which do you choose?

Now, imagine the exact same scenario, except now, the programs are slightly different. If you choose Program A, 400 people will die, and if you choose Program B, there is 1/3 probability that no one will die, and a 2/3 probability that 600 people will die. Which do you choose?

Just like the optical illusions above, the two problems are actually identical. The only change is the point of comparison. In the first case, we are dealing with lives saved, and in the second, with lives lost. What Tversky and Kahneman found, however, is that the answers are vastly different in the two cases. In the first, the majority of people choose Program A, a guarantee of saving lives. But in the second, when the frame is reversed, the majority of people choose Program B: When faced with the certainty of loss, they become risk-seeking.

Implications for mindful decisions

How information is presented matters more than we know. We can’t choose without having a point of comparison. And just as our eyes can deceive us in optical illusions, our brains can deceive us when we are making choices that are framed in different ways, or comparing options that have been presented in different sequences or contexts. There is really no way around it other than to be aware of it – and to take a moment before committing to a choice to really think about what it is you are choosing and why you are choosing it. Be especially wary with purchasing options. No one more so than marketers, advertisers, and retailers knows the power of the frame, and often, savvy marketers and stores can easily manipulate our preferences by mere presentation (one classic example is presenting a low, middle, and high option when you want people to gravitate to the middle one; it works like a charm).

So, the next time you make a choice, stop a moment and consider: What is my point of comparison? What are the other options? And are they influencing my perception in a way that is not immediately obvious? Am I looking at two identical lines, or two identical squares, and perceiving them as different? And if so, what can I do about it?