Does Making A Quantum Measurement Really Destroy Information?
The act of observing doesn’t just determine a previously indeterminate state, but can destroy information, too.
Imagine that you’re a scientist attempting to understand reality at a fundamental level. How would you go about exploring it? You’d attempt to break up the matter you’re dealing with into tiny, well-understood components. You’d design experiments to test and measure the properties of those tiny subatomic particles under a variety of conditions. And — if you were clever — you’d attempt to use the properties that you measured and the experiments you performed to learn exactly what rules the Universe obeyed.
In principle, you’d think, you could make enough measurements or perform enough experiments to learn as much as you wanted about any particle (or set of particles) in the entire Universe. Indeed, that was the expectation of many at the dawn of the 20th century. As it turned out, however, the quantum Universe had other ideas in store for us. Certain measurements, when you make them, completely invalidate the information you had learned from your prior measurement. The act of measuring, apparently, really does destroy information. Here’s how we figured it out.

In theory, the story starts with a basic idea from math: the notion of commutativity. Commutative means “you can move something around” and it doesn’t change. Addition is commutative: 2 + 3 = 3 + 2. Same thing with multiplication: 2 × 3 = 3 × 2. But subtraction isn’t: 2–3 ≠ 3–2, but rather you need to throw a negative sign in there to make the expression true. Division isn’t either, and is a little more complicated: 2 ÷ 3 ≠ 3 ÷ 2, and you’d need to take the reciprocal (the inverse) of one side to equal the other.
In physics, this idea of commutativity doesn’t just apply to mathematical operations, but to physical manipulations or measurements you can make as well. A simple example that we can look to is the idea of rotations. If you take an object that’s different along its three dimensions — like a cellphone — you can attempt to make two rotations:
- holding an object in front of you, rotate it 90 degrees counterclockwise about the axis facing you,
- then take that same object and rotate it 90 degrees clockwise about the vertical axis in front of you.
Perhaps surprisingly, the order in which you perform these two rotations really matters.

This idea of non-commutativity shows up even in the classical world of physics, but its most famous application comes in the quantum realm: in the form of the Heisenberg uncertainty principle. Here in our classical world, there are all sorts of properties of an object that we can measure at any moment in time. Put it on a scale, and you measure its mass. Put a motion sensor on it, and you can measure its momentum. Fire a set of lasers at it, and you can measure its position. Send it into a calorimeter, and you can measure its energy. And if you set up a stopwatch while it’s oscillating, you can measure the amount of time it takes to complete one full cycle.
Well, in the quantum Universe, many of these measurements are still valid at the particular instant you make them, but not forever. The reason is this: certain quantities that you can measure — pairs of observables known as conjugate variables — are inherently related to one another. If you measure momentum to a certain precision, you cannot inherently know your position to better than a certain specific accuracy, even if you previously measured your position more precisely than that previously.

The idea of Heisenberg uncertainty was unpalatable to many, and yet, the Universe seemed to mandate it. This extended to other sets of conjugate variables as well:
- position (Δx) and momentum (Δp),
- energy (ΔE) and time (Δt),
- electric potential, or voltage (Δφ) and free electric charge (Δq),
- or angular momentum (ΔL) and orientation, or angular position (Δθ).
However, if you really want to demonstrate the physical necessity of something, you absolutely have to obtain the experimental results to back it up. It isn’t necessarily enough to state something like “I don’t know how precisely I can trust my measurements,” you have to discover a way to reveal that information that you previously knew or measured to some degree of accuracy has been destroyed by the act of subsequent measurements.
In 1921, physicist Otto Stern came up with a brilliant idea to test exactly this.

Imagine that you have a quantum particle, like an electron, a proton, a composite nucleus: an object made up of protons and neutrons bound together, or even a neutral atom with a nucleus and electrons orbiting it. There are a number of quantum properties inherent to this object, such as mass, electric charge, etc. In theory, there should also be a form of angular momentum inherent to this particle as well, not merely from the fact that it orbits (or is orbited by) other particles, but intrinsic to itself in isolation. This quantum property is called spin, in analogy with the idea of a top rotating about its axis.
If you had a spinning top, you can immediately imagine two ways it could be spinning:
- clockwise about its vertical axis,
- or counterclockwise about its vertical axis.
If you lived in a world that wasn’t weighted down by gravity — where you have a preferred direction (towards the center of the Earth) that orients your spin axis — you could also imagine that it could be spinning either clockwise or counterclockwise about any axis at all in any of the three allowable dimensions. That’s the setup: the notion that the idea of spin, or intrinsic angular momentum, exists for these particles. Although 1921 was several years before Uhlenbeck and Goudsmit formulated their hypothesis of an electron’s spin, the notion was still present in the original “old quantum theory” of Bohr and Sommerfeld.
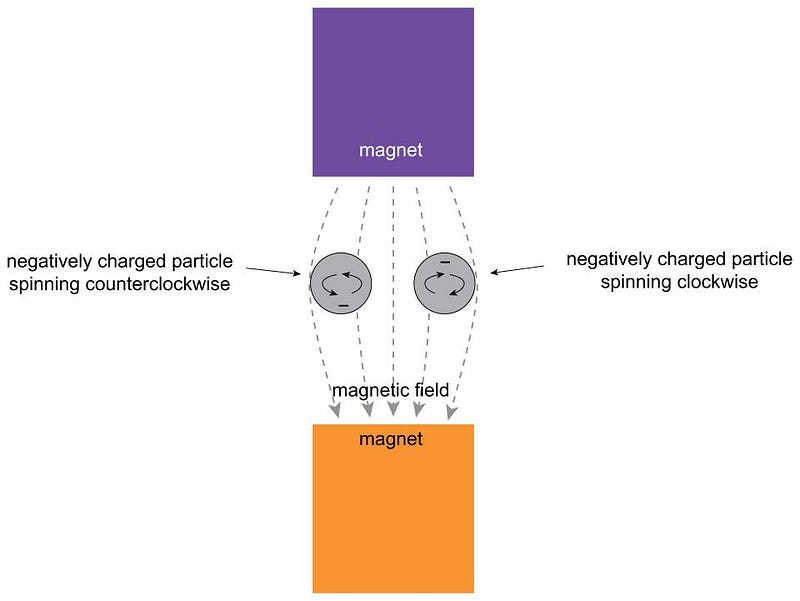
How could one measure the spin of quantum particles? And how, moreover, could you determine if spin was a continuous quantity capable of taking on any value, as the classical Universe predicted, or whether it was inherently quantum in nature, with only specific discrete values it could take on?
Stern realized that if you had a magnetic field that pointed in one particular direction that was perpendicular to the direction in which this charged, spinning particle was moving, the field would deflect the particle according to its magnetic moment, which would be related to its spin. A particle without any spin wouldn’t deflect, but a particle with spin (either positive or negative) would be deflected along the direction of the magnetic field.
If spin was quantized and discrete, you would only see specific locations where these particles, all moving at the same speed, would land. But if spin was classical and continuous, those particles could land absolutely anywhere.
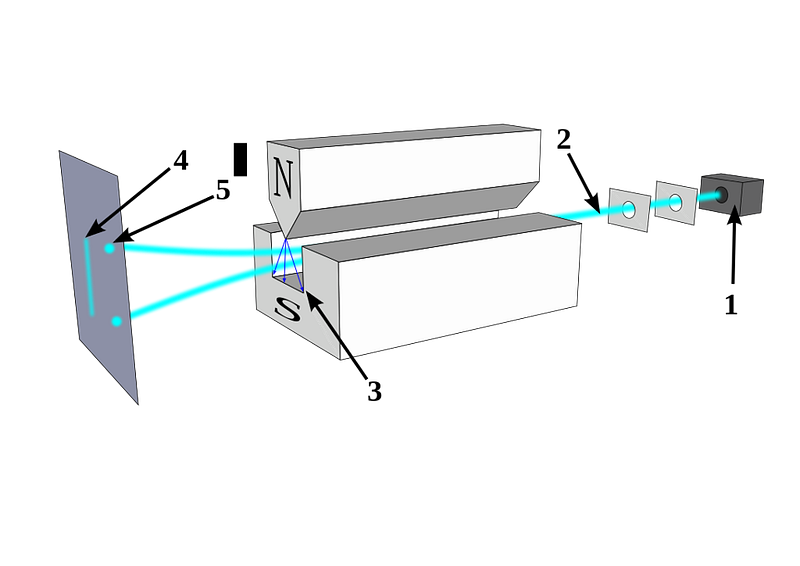
In 1922, physicist Walther Gerlach put Stern’s ideas to the test, devising what is now known as the Stern-Gerlach experiment. Gerlach started by setting up an electromagnet around a beam of silver atoms, which were easy to accelerate to a uniform speed. With the electromagnet turned off, the silver atoms all landed at the same location on a detector on the other side of the magnet. When the magnet was ramped up and turned on, the beam split into two: with half the atoms deflected along the direction of the magnetic field and half deflected opposed to the magnetic field. As we know today, this corresponds to spins of +½ and -½, aligned or anti-aligned with the magnetic field.
This early experiment was enough to prove that spin existed, and that it was quantized into discrete values. But what came next would really demonstrate the power of quantum mechanics to destroy previously known information. When you pass those silver atoms through a Stern-Gerlach apparatus with the field turned on, the beam of atoms splits in two, corresponding to spins in each of the two allowed directions.
What, then, would happen if you were to pass one of those two halves of the beam through another Stern-Gerlach experiment?
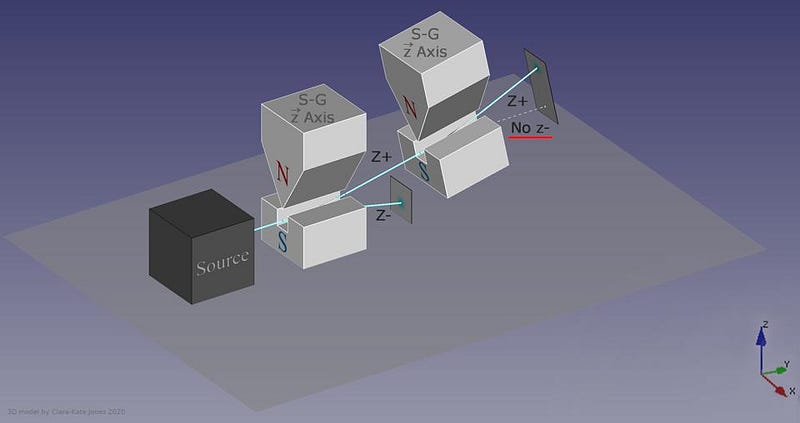
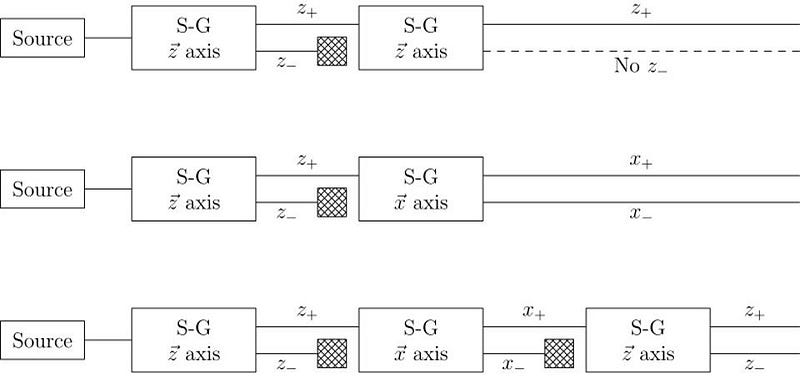
The answer, perhaps surprisingly, is that it depends on which direction your magnet is oriented. If your original Stern-Gerlach apparatus were oriented in, say, the x-direction, you’d get a split where some of the particles were deflected in the +x direction and others were deflected in the –x direction. Now, let’s only save the +x particles. If you pass them through another magnet that’s also oriented in the x-direction, the particles won’t split; they’ll all be oriented in the +x direction still.
But if you oriented your second magnetic field in the y-direction instead, you’d find something a little surprising. The beam of particles that originally had a +x orientation now split along the y-direction, with half deflecting in the +y direction and the other half deflecting in the –y direction.
Now, here’s where the critical moment occurs: what happens if you save, for example, only the +y particles, and pass them once again through a magnetic field oriented in the x-direction?
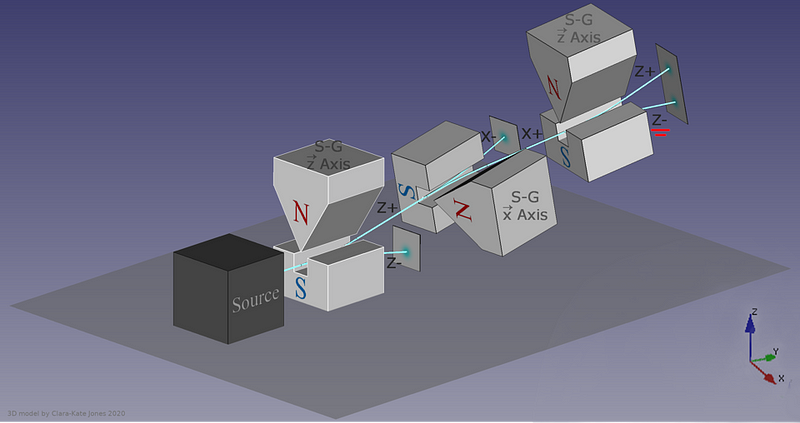
Once again, just like they did initially, they split into +x and –x directions. When you passed them through that second magnetic field, in a different (orthogonal) direction to the first magnetic field, you destroyed the information you obtained in your first measurement. As we now understand it today, the three different possible directions for spin angular momentum — the x, y, and z directions — all don’t commute with one another. Making a quantum measurement of one type of variable really does destroy any prior information about its conjugate variables.
The Stern-Gerlach experiment went on to have lasting implications. In 1927, it was shown that this splitting occurs even for hydrogen atoms, showing that hydrogen has a non-zero magnetic moment. Atomic nuclei themselves have a quantized angular momentum intrinsic to them, and also split in a Stern-Gerlach-like apparatus. By varying the magnetic field over time, scientists figured out how to force the magnetic moment to enter one state or another, with state transitions capable of being induced by a time-varying field. This led to the birth of magnetic resonance, still used ubiquitously in modern MRI machines, with subsequent applications of the key transition leading to atomic clocks as well.
The act of measurement and observation seems like it shouldn’t affect the outcome, as it’s a truly absurd idea that watching a system can alter its properties. But in the quantum Universe, this not only occurs, but was demonstrated before the theory was even fully understood. If you measure a particle’s spin along one direction, you destroy any previously-obtained information about the other two directions. Even if you had measured them previously and known them exactly, the act of making that new measurement fundamentally erases (or randomizes) any information you had gained earlier.
When many physicists first hear Einstein’s quip about how “God doesn’t play dice with the Universe,” this is the first experiment they should think of as a counterexample. No matter how well you think you understand reality — no matter how precisely or accurately you measure it in a variety of ways — the act of making any new measurement will intrinsically randomize some of the information you had pinned down just prior to your measurement. Making that new measurement really does destroy old information, and all you need is a magnet and some particles to prove that this is true.
Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.