Ask Ethan: Can We Really Get A Universe From Nothing?

And does it require the idea of ‘negative gravity’ in order to work?

The biggest question that we’re even capable of asking, with our present knowledge and understanding of the Universe, is where did everything we can observe come from? If it came from some sort of pre-existing state, we’ll want to know exactly what that state was like and how our Universe came from it. If it emerged out of nothingness, we’d want to know how we went from nothing to the entire Universe, and what if anything caused it. At least, that’s what our Patreon supporter Charles Buchanan wants to know, asking:

One concept bothers me. Perhaps you can help. I see it in used many places, but never really explained. “A universe from Nothing” and the concept of negative gravity. As I learned my Newtonian physics, you could put the zero point of the gravitational potential anywhere, only differences mattered. However Newtonian physics never deals with situations where matter is created… Can you help solidify this for me, preferably on [a] conceptual level, maybe with a little calculation detail?

Gravitation might seem like a straightforward force, but an incredible number of aspects are anything but intuitive. Let’s take a deeper look.

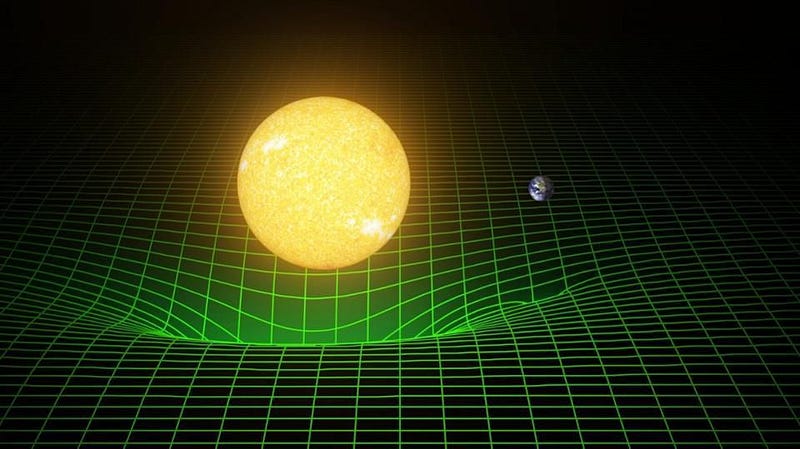
If you have two point masses located some distance apart in your Universe, they’ll experience an attractive force that compels them to gravitate towards one another. But this attractive force that you perceive, in the context of relativity, comes with two caveats.

The first caveat is simple and straightforward: these two masses will experience an acceleration towards one another, but whether they wind up moving closer to one another or not is entirely dependent on how the space between them evolves. Unlike in Newtonian gravity, where space is a fixed quantity and only the masses within that space can evolve, everything is changeable in General Relativity. Not only does matter and energy move and accelerate due to gravitation, but the very fabric of space itself can expand, contract, or otherwise flow. All masses still move through space, but space itself is no longer stationary.

The second caveat is that the two masses you’re considering, even if you’re extremely careful about accounting for what’s in your Universe, are most likely not the only forms of energy around. There are bound to be other masses in the form of normal matter, dark matter, and neutrinos. There’s the presence of radiation, from both electromagnetic and gravitational waves. There’s even dark energy: a type of energy inherent to the fabric of space itself.

Now, here’s a scenario that might exemplify where your intuition leads you astray: what happens if these masses, for the volume they occupy, have less total energy than the average energy density of the surrounding space?

You can imagine three different scenarios:

1. The first mass has a below-average energy density while the second has an above-average value.
2. The first mass has an above-average energy density while the second has a below-average value.
3. Both the first and second masses have a below-average energy density compared to the rest of space.

In the first two scenarios, the above-average mass will begin growing as it pulls on the matter/energy all around it, while the below-average mass will start shrinking, as it’s less able to hold onto its own mass in the face of its surroundings. These two masses will effectively repel one another; even though gravitation is always attractive, the intervening matter is preferentially attracted to the heavier-than-average mass. This causes the lower-mass object to act like it’s both repelling and being repelled by the heavier-mass object, the same way a balloon held underwater will still be attracted to Earth’s center, but will be forced away from it owing to the (buoyant) effects of the water.

So what’s going to happen if you have two regions of space with below-average densities, surrounded by regions of just average density? They’ll both shrink, giving up their remaining matter to the denser regions around them. But as far as motions go, they’ll accelerate towards one another, with exactly the same magnitude they’d accelerate at if they were both overdense regions that exceeded the average density by equivalent amounts.

You might be wondering why it’s important to think about these concerns when talking about a Universe from nothing. After all, if your Universe is full of matter and energy, it’s pretty hard to understand how that’s relevant to making sense of the concept of something coming from nothing. But just as our intuition can lead us astray when thinking about matter and energy on the spacetime playing field of General Relativity, it’s a comparable situation when we think about nothingness.

You very likely think about nothingness as a philosopher would: the complete absence of everything. Zero matter, zero energy, an absolutely zero value for all the quantum fields in the Universe, etc. You think of space that’s completely flat, with nothing around to cause its curvature anywhere.

If you think this way, you’re not alone: there are many different ways to conceive of “nothing.” You might even be tempted to take away space, time, and the laws of physics themselves, too. The problem, if you start doing that, is that you lose your ability to predict anything at all. The type of nothingness you’re thinking about, in this context, is what we call unphysical.

If we want to think about nothing in a physical sense, you have to keep certain things. You need spacetime and the laws of physics, for example; you cannot have a Universe without them.

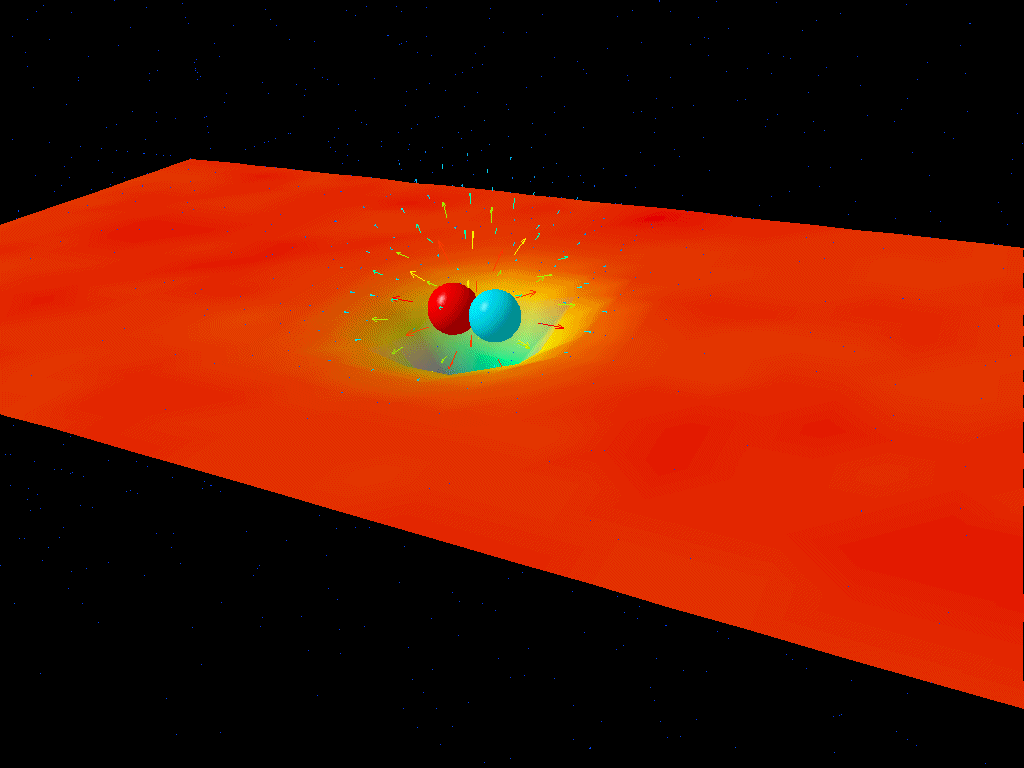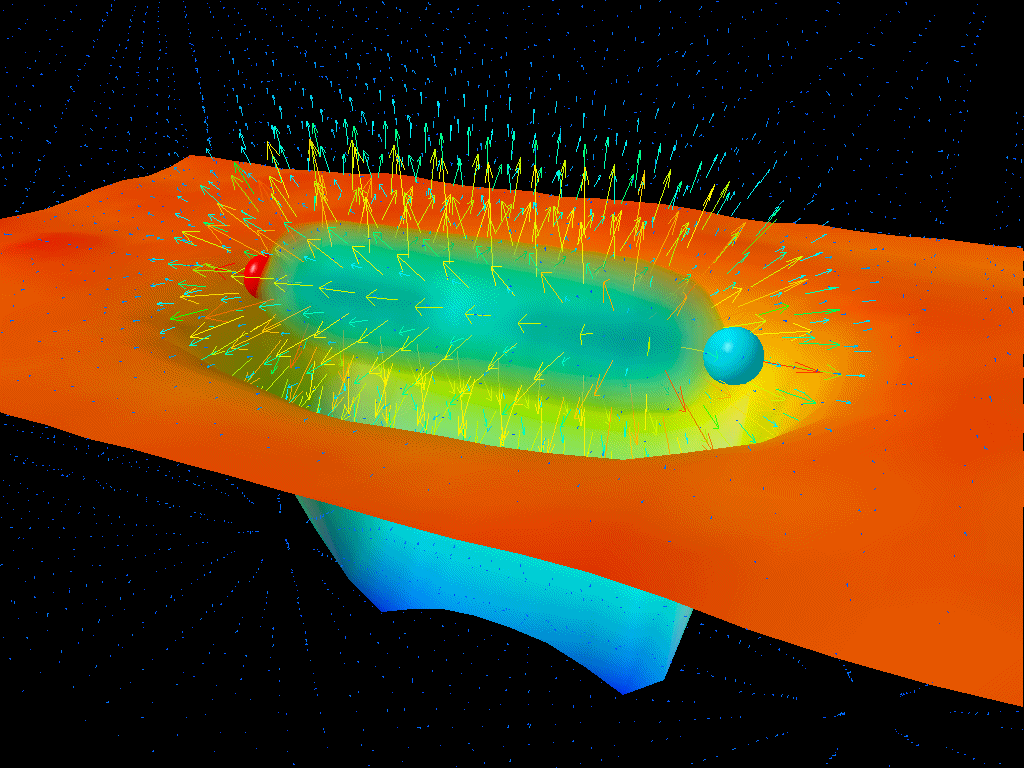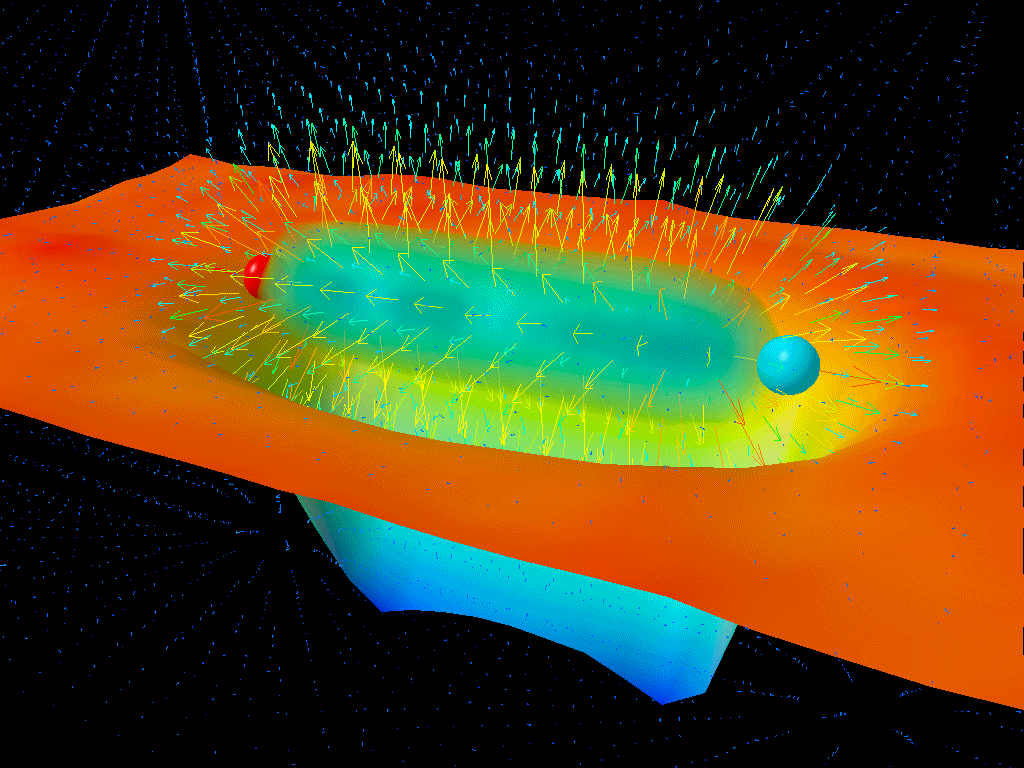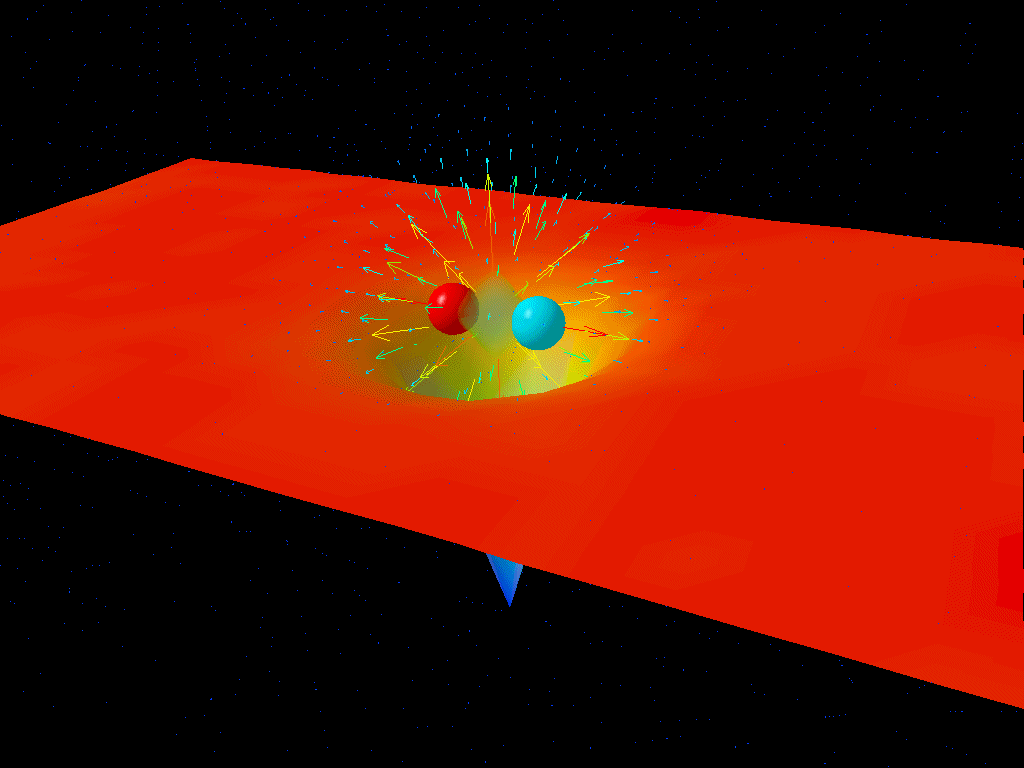
But here’s the kicker: if you have spacetime and the laws of physics, then by definition you have quantum fields permeating the Universe everywhere you go. You have a fundamental “jitter” to the energy inherent to space, due to the quantum nature of the Universe. (And the Heisenberg uncertainty principle, which is unavoidable.)

Put these ingredients together — because you can’t have a physically sensible “nothing” without them — and you’ll find that space itself doesn’t have zero energy inherent to it, but energy with a finite, non-zero value. Just as there’s a finite zero-point energy (that’s greater than zero) for an electron bound to an atom, the same is true for space itself. Empty space, even with zero curvature, even devoid of particles and external fields, still has a finite energy density to it.

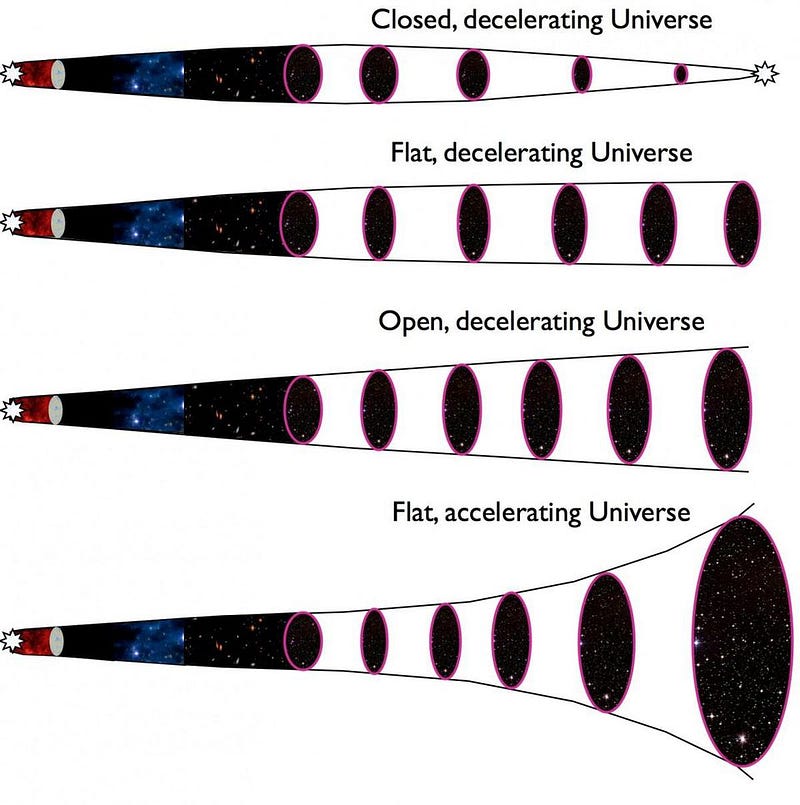
From the perspective of quantum field theory, this is conceptualized as the zero-point energy of the quantum vacuum: the lowest-energy state of empty space. In the framework of General Relativity, however, it appears in a different sense: as the value of a cosmological constant, which itself is the energy of empty space, independent of curvature or any other form of energy density.

Although we do not know how to calculate the value of this energy density from first principles, we can calculate the effects it has on the expanding Universe. As your Universe expands, every form of energy that exists within it contributes to not only how your Universe expands, but how that expansion rate changes over time. From multiple independent lines of evidence — including the Universe’s large-scale structure, the cosmic microwave background, and distant supernovae — we have been able to determine how much energy is inherent to space itself.

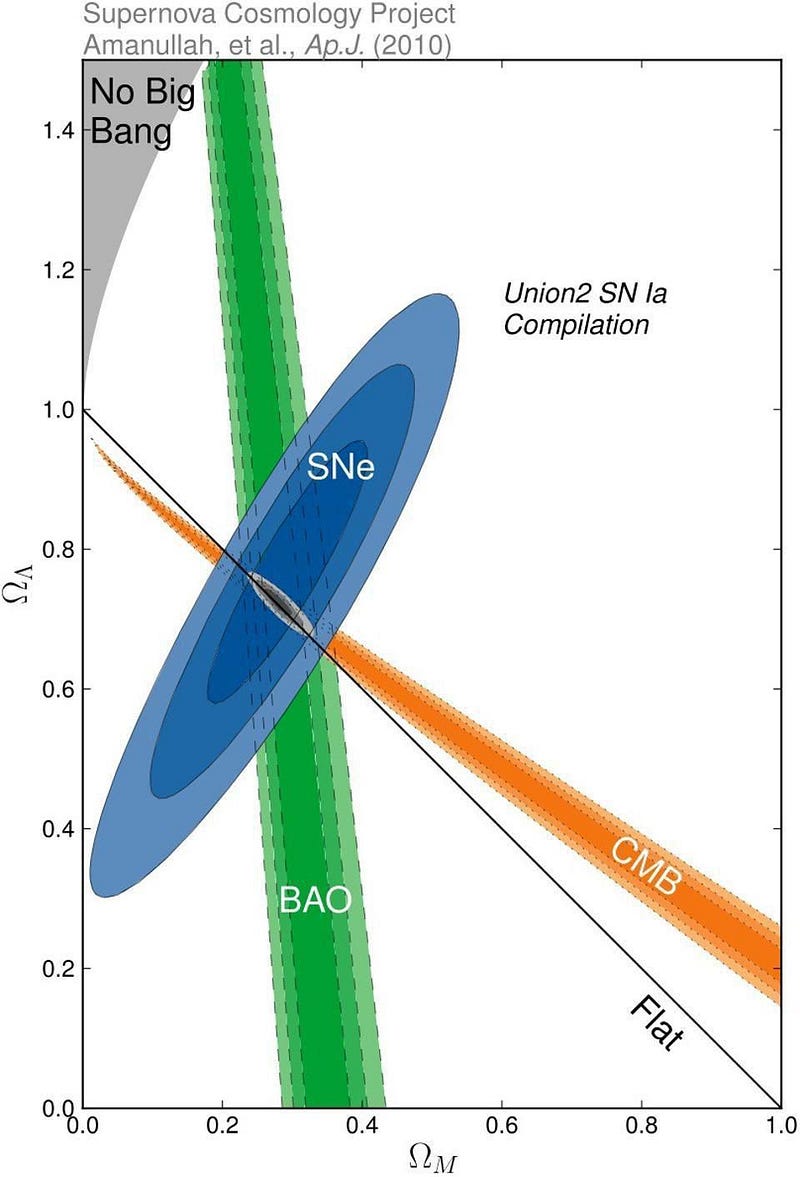
This form of energy is what we presently call dark energy, and it’s responsible for the observed accelerated expansion of the Universe. Although it’s been a part of our conceptions of reality for more than two decades now, we don’t fully understand its true nature. All we can say is that when we measure the expansion rate of the Universe, our observations are consistent with dark energy being a cosmological constant with a specific magnitude, and not with any of the alternatives that evolve significantly over cosmic time.

Because dark energy causes distant galaxies to appear to recede from one another more and more quickly as time goes on — since the space between those galaxies is expanding — it’s often called negative gravity. This is not only highly informal, but incorrect. Gravity is only positive, never negative. But even positive gravity, as we saw earlier, can have effects that look very much like negative repulsion.

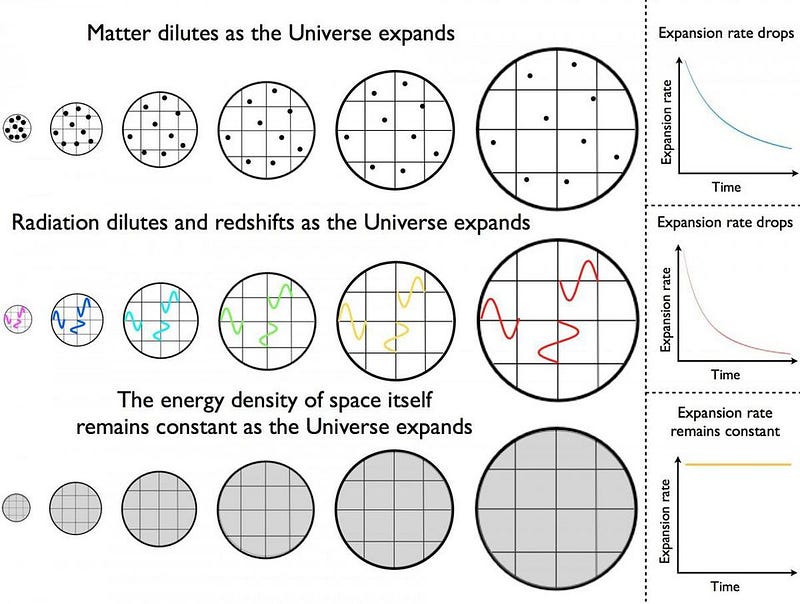
If there were greater amounts of dark energy present within our spatially flat Universe, the expansion rate would be greater. But this is true for all forms of energy in a spatially flat Universe: dark energy is no exception. The only different between dark energy and the more commonly encountered forms of energy, like matter and radiation, is that as the Universe expands, the densities of matter and radiation decrease.

But because dark energy is a property of space itself, when the Universe expands, the dark energy density must remain constant. As time goes on, galaxies that are gravitationally bound will merge together into groups and clusters, while the unbound groups and clusters will accelerate away from one another. That’s the ultimate fate of the Universe if dark energy is real.

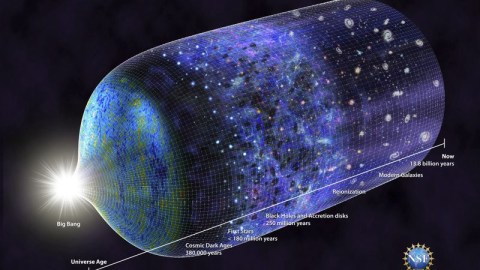
So why do we say we have a Universe that came from nothing? Because the value of dark energy may have been much higher in the distant past: before the hot Big Bang. A Universe with a very large amount of dark energy in it will behave identically to a Universe undergoing cosmic inflation. In order for inflation to end, that energy has to get converted into matter and radiation. The evidence strongly points to that happeningsome 13.8 billion years ago.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

When it did, though, a small amount of dark energy remained behind. Why? Because the zero-point energy of the quantum fields in our Universe isn’t zero, but a finite, greater-than-zero value. Our intuition may not be reliable when we consider the physical concepts of nothing and negative/positive gravity, but that’s why we have science. When we do it right, we wind up with physical theories that accurately describe the Universe we measure and observe.

Send in your Ask Ethan questions to startswithabang at gmail dot com!