Nature is not symmetric
We have electric charges and fields, but only magnetic fields. Could there be magnetic charges in our Universe?
“It is possible to commit no mistakes and still lose. That is not a weakness. That is life.” –Jean-Luc Picard
In science — particularly in physics — fundamental symmetries underlie a huge number of physical processes. In gravitation, the force that any mass exerts on another is equal and opposite to the force exerted by that second mass on the first.

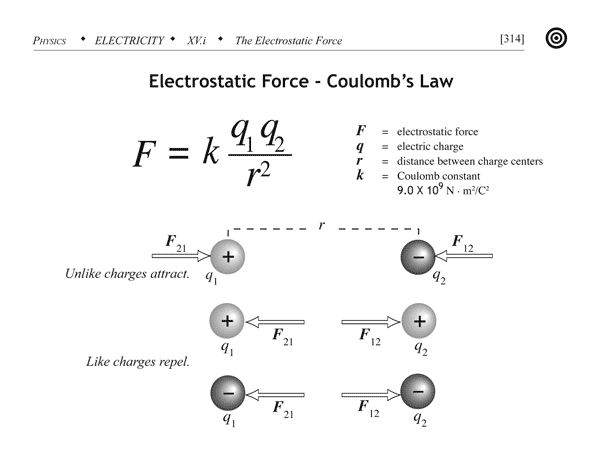
For electric charges, the same thing is true, although there’s an extra caveat: the electric force can either be positive or negative depending on the signs of the charges.
In addition, electricity is closely related to another force: magnetism.
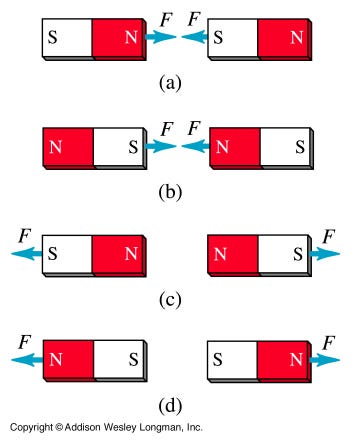
Just like electricity has positive and negative charges, where like repels like and opposites attract, magnetism has north and south poles, where like repels like and opposites attract.
But it appears that magnetism is fundamentally different from electricity in a particular (and obvious) way:
- In electricity, you can have many charges configured together or you can have a positive or negative charge in isolation, like an electron.
- But in magnetism, you can have many poles configured together but you can’t have an isolated “north pole” or “south pole” without the other.
In physics, when we have two, opposite charges or poles connected together, we call it a dipole, but when we have one by itself, we call it a monopole.
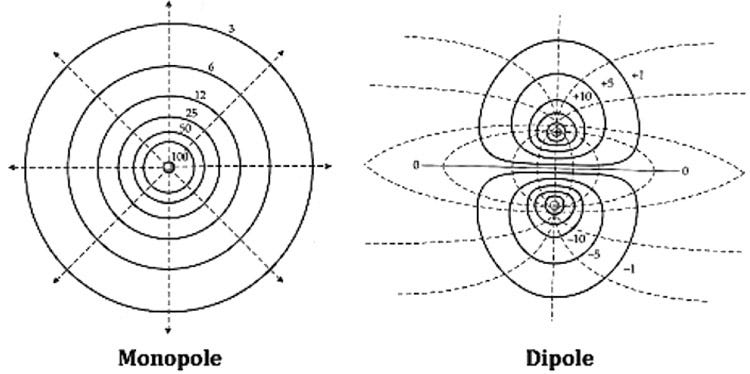
Gravitational monopoles are easy: it’s just a mass.
Electric monopoles are easy, too: any fundamental particle with a charge, like an electron or a quark, will do.
But magnetic monopoles? As far as we can tell, they don’t exist. Our Universe would be amazingly different, though, if they did. Think about, for a moment, how electricity and magnetism are related.
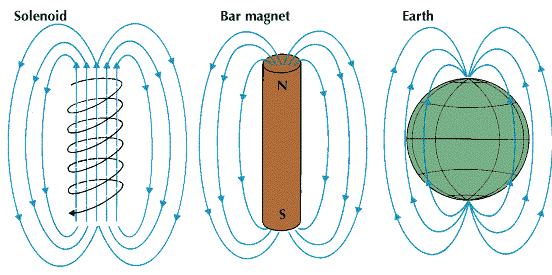
If you have a moving electric charge, also known as an electric current, it creates a magnetic field perpendicular to the charge’s movement.
If you have a straight wire with electric current flowing through it, it produces a magnetic field in a circle around the wire, while if you bend the current-carrying wire into a loop or coil, you create a magnetic field inside.
As it turns out, this goes both ways; like I said, the laws of physics tend to be symmetric. This means that if I have a loop (or coil) of wire, and I change the magnetic field inside of it, it will create an electric current in the loop, causing electric charges to move! This is the principle of electromagnetic induction, discovered by Michael Faraday more than 150 years ago.
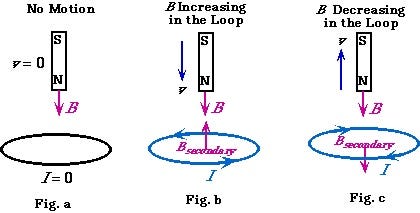
So you can have electric charges, electric currents and electric fields, but there are no magnetic charges or magnetic currents, only magnetic fields.
You can change a magnetic field to make electric charges move, but you can’t make magnetic charges move by changing an electric field because there are no magnetic charges.
Similarly, you can create a magnetic field by moving an electric charge, but you can’t create an electric field by moving a magnetic charge, again because there are no magnetic charges.
In other words, there’s a fundamental asymmetry between the electric and magnetic properties of our Universe. It’s why Maxwell’s equations for “E” and “B” fields (electric and magnetic fields) look so different from one another.

The reason these equations look so different is because electric charges (the ρ and the Q) and currents (the J and the I) exist, but their magnetic counterparts do not. If you take them away — the electric charges and currents — they would be symmetric, up to a factor of some fundamental constants relating them.
But what if magnetic charges and currents did exist? Physicists have wondered about this for more than a century, and assuming that they did, we could just write down what Maxwell’s equations would look like if there were such a thing as magnetic monopoles. Here’s what it would look like (in differential form only), below.
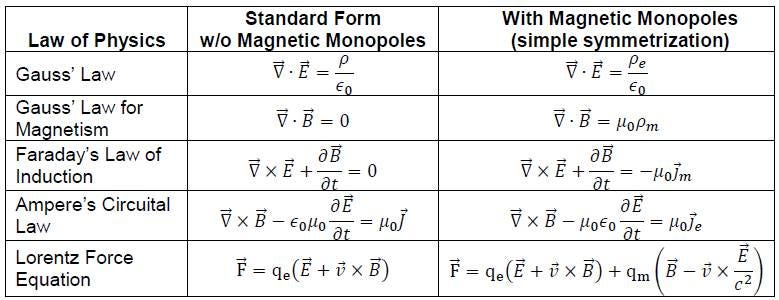
Again, except for some fundamental constants, the equations now look very symmetric! We’d be able to make magnetic charges move simply by changing electric fields, we’d be able to create magnetic currents and induce electric fields simply by doing so. Dirac played around with them in the 1930s, but it was generally recognized that they ought to leave some signature behind if they existed. None of this was taken seriously, however, because physics is at its core an experimental science; without any evidence of magnetic monopoles, it’s pretty hard to justify them.
But that began to change in the 1970s. People were experimenting with Grand Unified Theories, or the ideas that there might be more symmetry to nature that we presently see. The symmetries might be badly broken today, leading to our Universe that has four separate fundamental forces, but perhaps they were all unified at some high energy into one unique force? A consequence that all of these theories have is the existence of new, high energy particles, and in many incarnations, magnetic monopoles (specifically, `t Hooft / Polyakov monopoles) were predicted to exist.
Magnetic monopoles have always been an enticing possibility for physicists, but these new theories renewed interest. So in the 1970s, there were searches going on for them, and the most famous one was led by a physicist named Blas Cabrera. He took a long wire and made eight loops out of it, designed to measure magnetic flux through it. If a monopole passed through it, he would get a signal of exactly eight magnetons. But if a standard dipole magnet passed through it, he’d get a signal of +8 followed immediately by one of -8, so he could tell these apart.

So he built this device and waited. The device wasn’t perfect, and occasionally one of the loops would send a signal, and on even rarer occasions, two loops would send a signal at once. But you’d need eight (and exactly eight) for it to be a magnetic monopole. The apparatus never detected three or more. This experiment ran for some months with no success, and was eventually relegated to being checked up on only a few times a day. In February of 1982, he didn’t come in on Valentine’s Day. When he came back to the office on the 15th, he surprisingly found that the computer and the device had recorded exactly eight magnetons on February 14th, 1982.
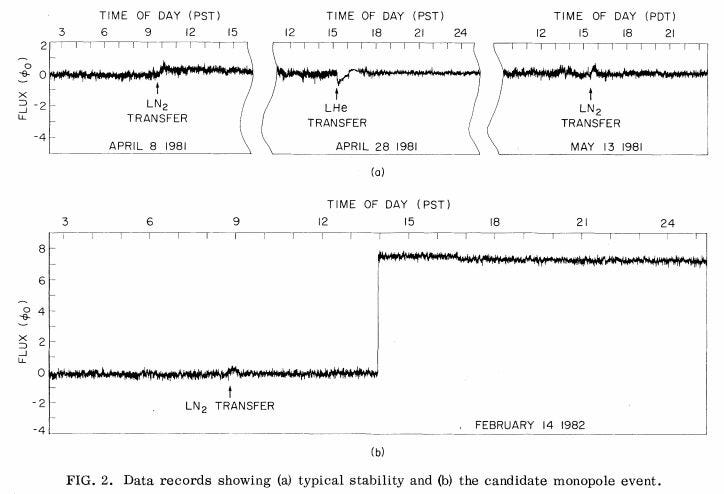
The discovery roared through the community, generating a huge amount of interest. Huge devices with larger surface areas and more loops were built, but despite extensive searching, another monopole was never seen. Stephen Weinberg even wrote Blas Cabrera a poem on February 14th, 1983:
Roses are red,
Violets are blue,
It’s time for monopole
Number TWO!
But monopole number two never came. Was it just an ultra-rare glitch that Cabrera’s experiment experienced? Was it the one-and-only magnetic monopole in our section of the Universe that just happened to pass through his detector? As we’ve never detected another, it’s impossible to know, but science needs to be reproducible to be accepted. And this experiment simply wasn’t able to be replicated.
Today, experiments still look for them, but the limits are insanely low.
As beautiful as it would be, and as much as we might expect it, nature just isn’t symmetric, not at all levels. And that’s no one’s fault; it’s just the way our Universe happens to be. Better to accept it as it actually is — no matter how aesthetically pleasing it would be were it different — than to let our predispositions guide us astray.
Leave your comments at the Starts With A Bang forum on Scienceblogs!





