Why are we made of matter and not antimatter?

The laws of physics appear to be symmetric between matter and antimatter. But the Universe tells a different story.
“If you see an antimatter version of yourself running towards you, think twice before embracing.” –J. Richard Gott III
When we look around at the Universe:
- at the planets and stars,
- at the galaxies and clusters of galaxies,
- and at the gas, dust and plasma populating the space between these dense structures,
we find the same signatures everywhere. We see atomic absorption and emission lines, we see matter interacting with other forms of matter, we see star formation and stellar death, collisions, X-rays and so much more.

But what we don’t see is just as important: we don’t see any signatures of matter annihilating with antimatter on the largest scales. We don’t see any evidence that some of these stars, galaxies or planets are made of antimatter. We don’t see the characteristic gamma rays that we’d expect to see if some antimatter parts were colliding (and annihilating) with the matter parts. Instead, it’s matter, matter everywhere, in the same abundance everywhere we look.
And this wouldn’t be such a problem for us, if it weren’t for one pesky fact: despite what E=mc^2 tells us — that you can make mass out of pure energy — all of the reactions and laws we know in the Universe today can only create mass by creating equal amounts of matter and antimatter.
So how did we get here today, with a Universe made of a lot of matter and practically no antimatter, if the laws of nature are completely symmetric between matter and antimatter? Well, there are two options: either the Universe was born with more matter than antimatter, or something happened early on, when the Universe was very hot and dense, to create a matter/antimatter asymmetry where there was none initially. While we can’t rule out the first option, we can’t exactly test that one out without literally re-inventing the Universe. But if the second one is true — if we made a matter/antimatter asymmetry where there was none initially — we have a lot of hope for figuring out how that happened.

The first major step towards this came in 1968, when the Soviet physicist Andrei Sakharov realized that if the Universe met just three conditions, making a matter/antimatter asymmetry was inevitable. The three conditions are as follows:
- The Universe must be out-of-equilibrium.
- The Universe must violate C- and CP-symmetry.
- And the Universe must possess interactions that violate baryon number.
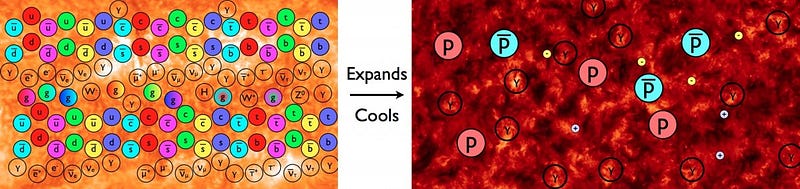
The first one is very, very easy: the Universe is perhaps the ultimate out-of-equilibrium state! As it expands, it cools, and reactions and interactions which occurred freely, easily and stably — like forming matter/antimatter pairs from the collisions of photons — suddenly ceased as the Universe became less hot and dense. As the Universe continues to expand and cool, it gets further and further from its prior, closer-to-equilibrium state.
And the second one, despite your reservations, is pretty easy, too. C symmetry says that if you replace particles with antiparticles, they should do the same thing. If you have a particle spin clockwise, the antiparticle should spin clockwise. If you have a particle decay in a certain way, the antiparticle should decay in the same way. But if C is violated, particle and antiparticles can behave opposite to one another! In practically all of the weak interactions (including radioactive decays), C is observed to be violated.
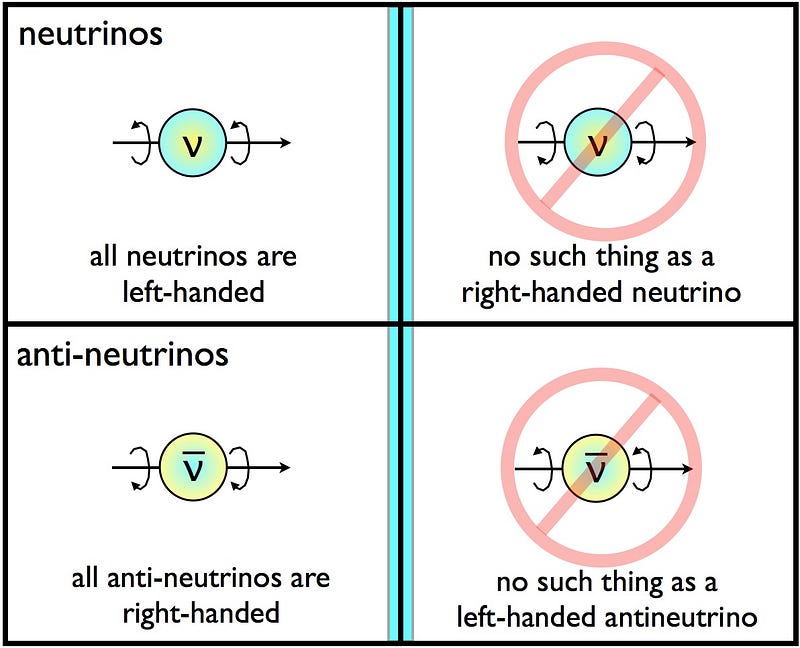
CP is a combination of C symmetry, where you replace particles with antiparticles, and P symmetry, where you reflect whatever happens in a mirror. Your left hand and your right hand exhibit P symmetry from one another: if you point your thumb up and curl your fingers, your left and right hands mirror one another. In particle physics, if you have a particle spinning clockwise and decaying upwards, its antiparticle should spin counterclockwise and decay upwards 100% of the time if CP is conserved. If not, CP is violated.
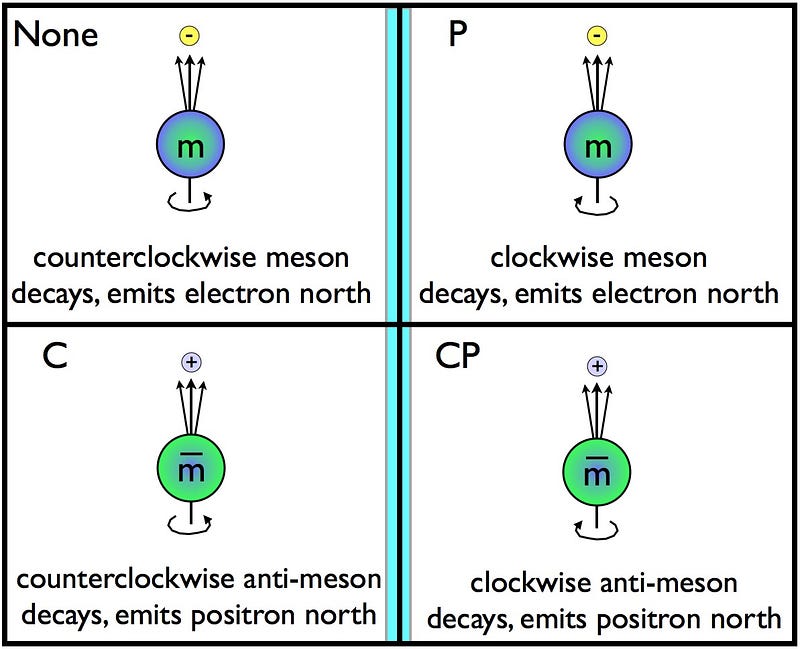
In nature, we’ve observed particles containing heavy quarks — strange, charm and bottom — to violate CP when they decay. But we’ve never observed the third Sakharov condition: a violation of Baryon Number (B). Strictly speaking, though, the Standard Model is only mandated to conserve B — L, or Baryon Number (B) minus Lepton Number (L). And in many extensions of the Standard Model, such as with new electroweak physics, with new high-energy lepton physics, with supersymmetry or with Grand Unification, large amounts of baryon violation are possible.

To show you how this might work in the early Universe, let’s consider that in a Grand Unified theory, there are two new types of particles: an X, with a charge of +4/3 and a B — L number of +2/3 (and an anti-X, with a charge of -4/3 and a B — L number of -2/3), and a Y, with a charge of -1/3 and a B — L number of -2/3 (and an anti-Y, with a charge of +1/3 and a B — L number of +2/3). These particles, in the hot, early Universe, are created in equal numbers so long as the Universe has enough energy to make them. They’re not the only thing that’s around, but they’re plentiful.
As the Universe expands and cools (this is the out-of-equilibrium part), we stop making them. Some of them will find one another and annihilate, while others will decay away. There are rules to how they decay:
- the total decay times of particles (X, Y) and antiparticles (anti-X, anti-Y) must be the same.
- any individual decay path that a particle can take (X or Y) must have its “anti” counterpart taken by the antiparticle (anti-X or anti-Y).
But there’s one exceptional thing that can happen when CP is violated:
- the individual decay paths between particles and antiparticles does not have to occur in the same fractions.
In other words, if a particle can decay in two different ways with a certain chance of each decay happening, its antiparticle must decay in those same corresponding ways, but the chances of each decay happening can be different!
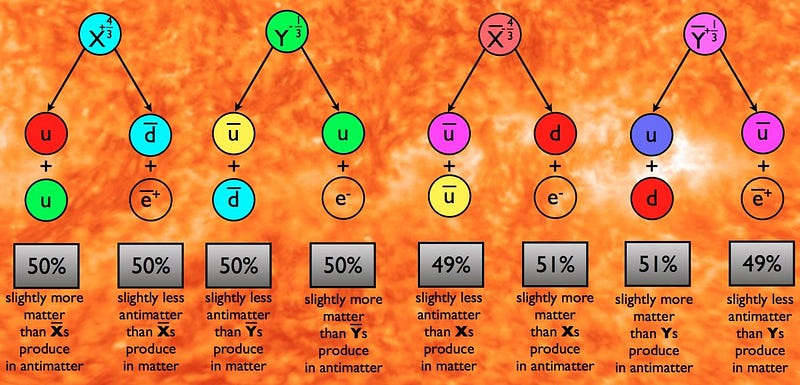
Look at the diagram above. We could have the X decay into two up quarks 50% of the time and into an antidown quark and a positron 50% of the time, but the anti-X decay into two antiup quarks only 49% of the time, while it can decay into a down quark and an electron 51% of the time. That would mean, for every 50 X and anti-X pairs that we created, we would get a total of 151 quarks, 51 leptons, 148 antiquarks and 50 antileptons. The quark–antiquark pairs and the lepton–antilepton pairs would annihilate away, leaving us with three quarks and one lepton left over, or the equivalent of one extra baryon (a proton or neutron) and one extra lepton (an electron or a neutrino). This pathway would allow us to create a significant asymmetry of matter over antimatter!
We can follow a similar analysis for the Y and anti-Y particles, and wind up with a Universe that has an asymmetry of matter over antimatter where there was none initially.
It is not yet decided exactly how this happens in our Universe, although if either the “new physics at the electroweak scale” or the “SUSY” explanation is correct, the LHC could find evidence for that as Run II — at the highest energies ever — continues in 2016. For those of you who enjoy podcasts, I have a much longer, more detailed version of this story for you to listen to below.
This is right at the frontiers of what is known, and is my bet for the next ofthe greatest unsolved problems in theoretical physics to fall. With any luck, we’ll finally be able to explain why there’s more matter than antimatter in our Universe very soon.
Leave your comments on our forum, and check out our first book: Beyond The Galaxy, available now, as well as our reward-rich Patreon campaign!





