This Simple Thought Experiment Shows Why We Need Quantum Gravity

If our current laws of physics can’t predict what will happen, even probabilistically, we need something new.
There are two theories we have that explain all the particles and their interactions in the known Universe: General Relativity and the Standard Model of particle physics. General Relativity describes gravity perfectly everywhere we’ve ever looked. From the smallest-scale attractions we’ve ever measured in a laboratory to the expansion and curvature of space due to Earth, the Sun, black holes, galaxies, or the entire Universe, our observations and measurements have never deviated from what we’ve observed. The Standard Model is equally successful for the other three forces: electromagnetism and the strong and weak nuclear forces. Every experiment, measurement, and observation has agreed perfectly with these two theories.
It sounds great, until you try to combine the two. If we do that, it all falls apart. The solution? We need a quantum theory of gravity. Here’s why.
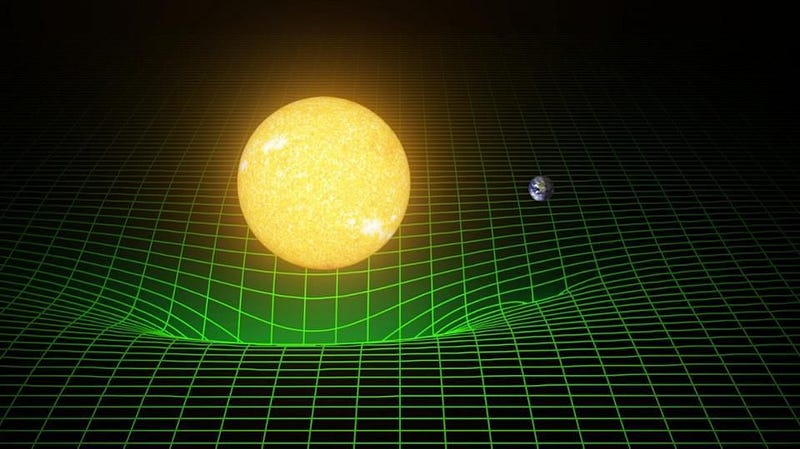
From Einstein’s theory of gravity, we can compute what the curvature of space is at any location in the Universe, from here on planet Earth to the largest scales in the cosmos. We’ve performed experiments that have tested the gravitational force law down to micron-sized scales, and on astrophysical scales in extreme environments, such as the galactic center, merging neutron stars, and at the edges of black holes. Even esoteric predictions, such as the production of gravitational waves, the effect of frame-dragging, or the precession of planetary orbits, are completely in line with every measurement we’ve ever taken. In every case, Einstein’s theory perfectly describes reality.
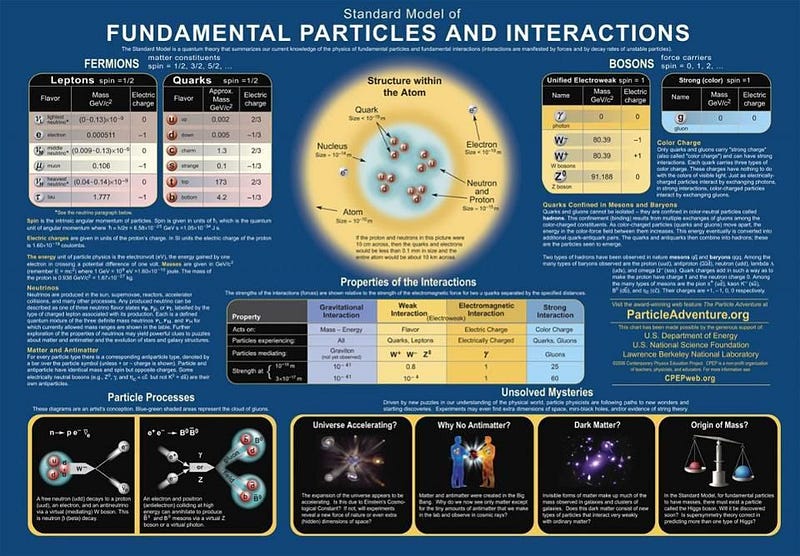
From the Standard Model, we know how electricity, magnetism, radioactive decays and nuclear forces work. Take any particle and let it interact (or not) with anything else in the Universe, and we’ll know the probability distribution of all possible outcomes. Even though the quantum world isn’t entirely deterministic, we can still successfully describe the expected set of outcomes in a mathematically precise fashion. If we perform the same experiment thousands upon thousands of times, we’ll see the results match our best quantum predictions, even for bizarre and unintuitive setups.
But if we take a look at one such setup in particular — the famed double-slit experiment — we can see immediately why a quantum theory of gravity is absolutely necessary.
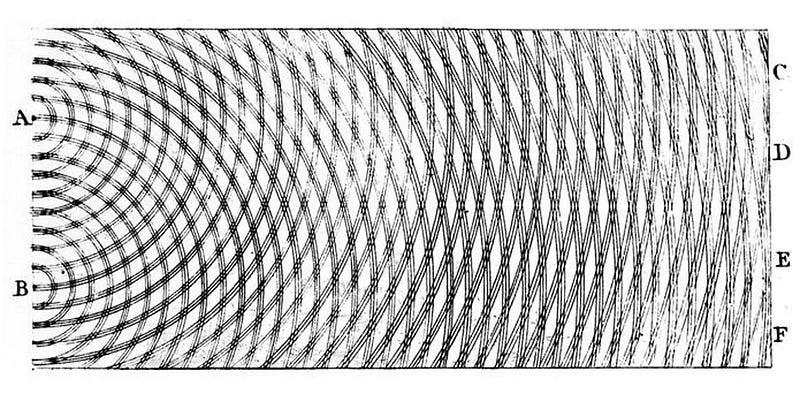
Imagine you’ve got a set of quantum particles: they could be photons, neutrinos, electrons, or anything else. Imagine that you’ve set them up so they’ll bombard a tiny area of a barrier, with two slits cut into the barrier extremely close together, to allow these quantum particles to pass through. Behind the barrier, you’ll set up a screen, so you can detect where the particles wind up. This is the classic setup of the double slit experiment.
If you send through a bunch of particles at once, they act just like a wave. The particles might go through one slit or the other, but they interfere. At the end of the day, you wind up with a clearly identifiable interference pattern on the screen, the same way you would for a water wave passing through a similar set of slits.

Well, you can’t have your particles interfering with one another, so you decide to send them through one-at-a-time. You measure where it hits the screen and record it, and then you fire the next particle. It doesn’t matter which particle you choose; if we can detect it on the screen, we see the same behavior. The interference pattern builds up one-particle-at-a-time, but clearly emerges. Somehow, these quantum particles are passing through both slits simultaneously, and are interfering with themselves.
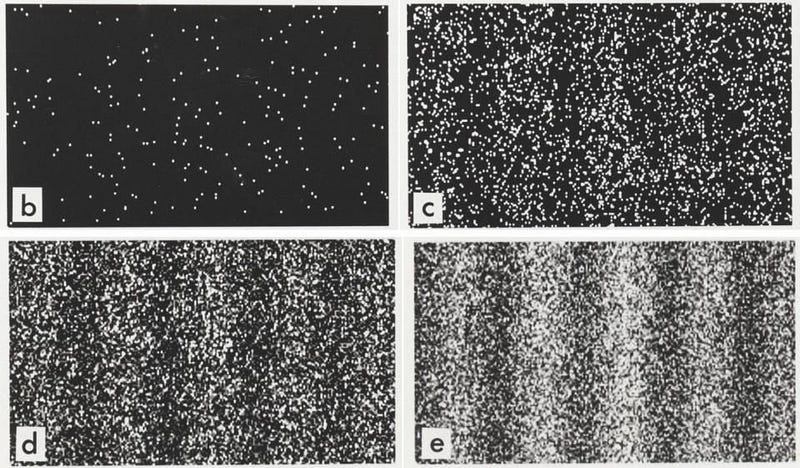
Perhaps you decide you’re not a fan of this quantum weirdness, so you decide to measure which slit each particle goes through. You set up a photodetector around each slit, and measure when a particle passes through it. The first particle goes through, and you detect its passage through slit #2. The second one arrives, and also goes through slit #2. The third one goes through slit #1, then the fourth through #2, and then the fifth through #1 again. You repeat this, over and over, for thousands of particles. And when you look at the resulting pattern on the screen, you find something extremely troublesome: the interference pattern is gone. Instead, all you see is a pile of particles that passed through slit #1, along with another pile that passed through slit #2. They did not interfere.
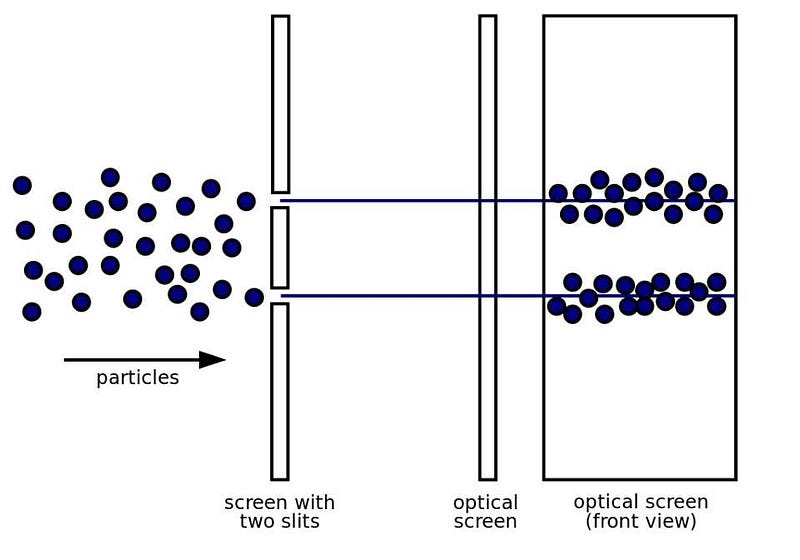
This is weird! This unintuitive weirdness is at the heart of what makes quantum physics, and the Standard Model in general, such a powerful tool. At a fundamental, quantum level, we can accurately predict when you have this quantum behavior and when you won’t, and what that behavior will look like when it appears.
For the electromagnetic, strong nuclear, and weak nuclear forces, this works exquisitely well. It works so well that, as bizarre as they may be, no repeatable experiment has ever disagreed with any significance from the Standard Model’s predictions. And yet, if we were to ask the following simple question, we don’t have any way to arrive at an answer:
What happens to the gravitational field of an electron when it passes through a double slit?

The reason we can’t answer it is we don’t know a huge number of properties about gravity on the quantum scale. We don’t know whether gravity is quantized or not. The particles must be quantized, but gravity might not be, and if it isn’t, the double slit experiment would give different results than if it is.
We don’t know whether space is fundamentally discrete (with a minimum length scale) or continuous. If there were a minimum length, there would be a fundamental resolution limit to our experiments, one we might someday encounter at high enough energies. There are questions we cannot answer about how gravity behaves under certain experimental conditions.

We know, in principle, that the gravitational field should remain localized around the electron’s position, just as it would for any mass. But what does this mean when the electron’s position is inherently uncertain? Does the gravitational field always go primarily through one slit or the other? And does the act of observing (or not observing) change the gravitational field? And if so, how?
The gravitational field of the electron is weak; we cannot observe it in practice. Equations developed by Wheeler, Feynman, and DeWitt in the 1960s describe the expected behavior of a particle in the weak-field limit of quantum gravity, but those equations have never been experimentally tested. To do so is presently beyond the realm of what we’re capable of, but there is hope.
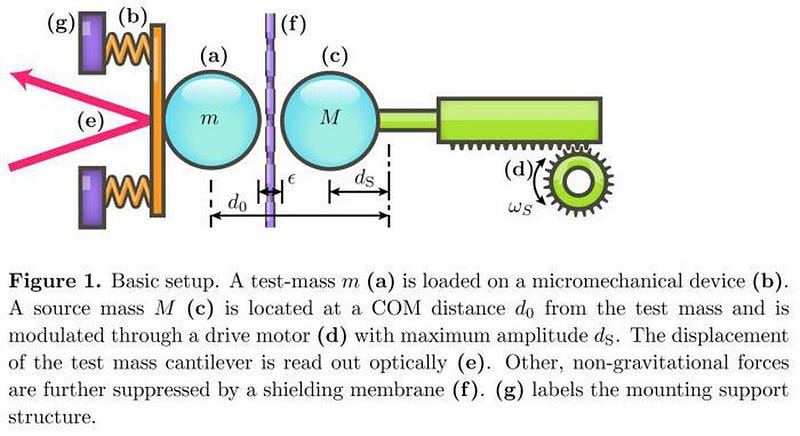
There are proposed experimental setups that would allow us to measure the gravitational field more precisely than ever before: down to milligram masses. On the other hand, we’ve managed to bring relatively large objects (compared to fundamental particles) into quantum superpositions of states: up to nanogram-scale masses. The exact energy levels of these states depend on the total gravitational self-energy of the system, making this a realistic, plausible test to determine whether gravity is quantized or not. When technology and experimental techniques advance far enough, these two scales will intersect. When that moment comes, we’ll be able to probe the quantum gravitational regime.
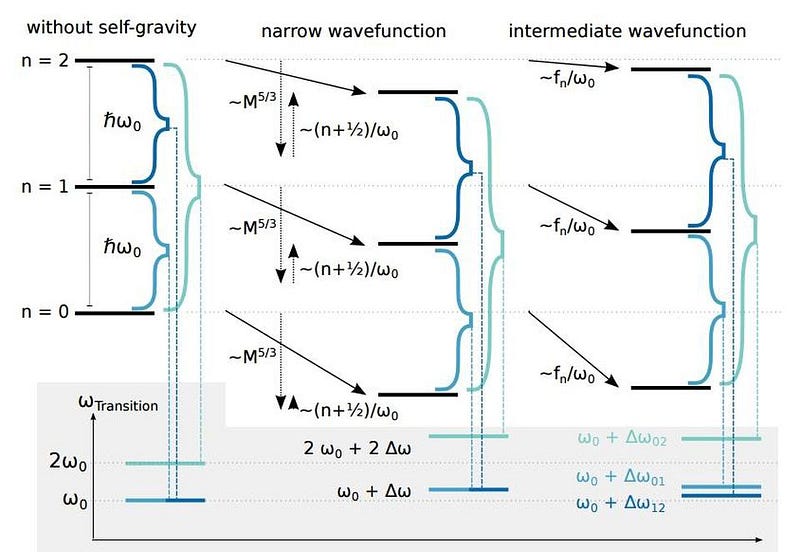
The description that General Relativity puts forth — that of matter telling space how to curve, and curved space telling matter how to move — needs to be augmented to include an uncertain position that has a probability distribution to it. Whether gravity is quantized or not is still an unknown, and has everything to do with the outcome of such a hypothetical experiment. How an uncertain position translates into a gravitational field, exactly, remains an unsolved problem on the road to a full quantum theory of gravity. The principles that underlie quantum mechanics must be universal, but how those principles apply to gravity, and in particular to a particle passing through a double slit, is a great unknown of our time.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.





